题目内容
 如图,已知∠1+∠D=90°,BE∥FC,且DF⊥BE与点G,并分别于AB、CD交于点F、D,求证:AB∥CD.
如图,已知∠1+∠D=90°,BE∥FC,且DF⊥BE与点G,并分别于AB、CD交于点F、D,求证:AB∥CD.考点:平行线的判定与性质
专题:证明题
分析:先根据垂直的定义可得∠1+∠D=90°,则根据等角的余角相等得∠1=∠2,接着根据平行线的性质,由BE∥CF得到∠2=∠C,则∠1=∠C,然后根据平行线的判定可得AB∥CD.
解答:证明:∵DF⊥BE,
∴∠1+∠D=90°,
而∠1+∠D=90°,
∴∠1=∠2,
∵BE∥CF,
∴∠2=∠C,
∴∠1=∠C,
∴AB∥CD.
∴∠1+∠D=90°,
而∠1+∠D=90°,
∴∠1=∠2,
∵BE∥CF,
∴∠2=∠C,
∴∠1=∠C,
∴AB∥CD.
点评:本题考查了平行线的判定与性质:平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在3×3的网格图中,在不添加其他线的情况下,不是正方形的矩形个数为( )
如图,在3×3的网格图中,在不添加其他线的情况下,不是正方形的矩形个数为( )| A、14个 | B、22个 |
| C、36个 | D、以上都不正确 |
若两个相似多边形的面积之比为1:4,则它们的周长之比为( )
| A、1:4 | B、1:2 |
| C、2:1 | D、1:16 |
下列图案中,可以看作是中心对称图形的有( )

| A、1个 | B、2个 | C、3个 | D、4个 |

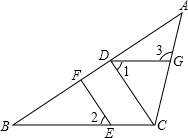 如图,在△ABC中,点E、G分别在BC、AC上,CD⊥AB,EF⊥AB,垂足分别为D、F.已知∠1+∠2=180°,∠3=105°,求∠ACB的度数.请将求∠ACB度数的过程填写完整.
如图,在△ABC中,点E、G分别在BC、AC上,CD⊥AB,EF⊥AB,垂足分别为D、F.已知∠1+∠2=180°,∠3=105°,求∠ACB的度数.请将求∠ACB度数的过程填写完整.