题目内容
4.$\sqrt{a+2\sqrt{a-1}}$+$\sqrt{a-2\sqrt{a-1}}$.分析 先配方得到:原式=$\sqrt{(\sqrt{a-1}+1)^{2}}$+$\sqrt{(\sqrt{a-1}-1)^{2}}$,再利用二次根式的性质化简得到原式=|$\sqrt{a-1}$+1|+|$\sqrt{a-1}$-1|,然后根据a的取值范围去绝对值后合并即可.
解答 解:原式=$\sqrt{a-1+2\sqrt{a-1}+1}$+$\sqrt{a-1-2\sqrt{a-1}+1}$
=$\sqrt{(\sqrt{a-1}+1)^{2}}$+$\sqrt{(\sqrt{a-1}-1)^{2}}$
=|$\sqrt{a-1}$+1|+|$\sqrt{a-1}$-1|,
当1≤a≤2时,原式=$\sqrt{a-1}$+1+1-$\sqrt{a-1}$=2;
当a>2时,原式=$\sqrt{a-1}$+1+$\sqrt{a-1}$-1=2$\sqrt{a-1}$.
点评 本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.利用配方法变形是解决此题的关键.

练习册系列答案
相关题目
14.等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边为( )
| A. | 7cm | B. | 7cm或5cm | C. | 5cm | D. | 3cm |
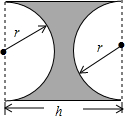 一零件的横截面(阴影部分)如图所示,你能用关于r,h的多项式表示此零件的横截面积吗?这个多项式能分解因素吗?若r=4cm,h=10cm,求这个零件的横截面积.(结果精确到个位).
一零件的横截面(阴影部分)如图所示,你能用关于r,h的多项式表示此零件的横截面积吗?这个多项式能分解因素吗?若r=4cm,h=10cm,求这个零件的横截面积.(结果精确到个位).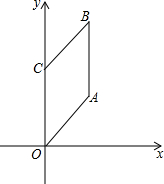 如图,在菱形OABC中,点O为坐标原点,点C在y轴上,且A(3,4).
如图,在菱形OABC中,点O为坐标原点,点C在y轴上,且A(3,4). 如图,在△ABC中,AB=AC,∠A=40°,BD是∠ABC的平分线,求∠BDC的度数.
如图,在△ABC中,AB=AC,∠A=40°,BD是∠ABC的平分线,求∠BDC的度数.