题目内容
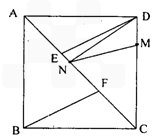
(Ⅰ)若E、F为AC的三等分点,求证:∠ADE= ∠CBF;
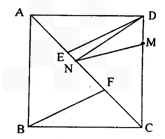
(Ⅱ)若M是DC上一点,且DM=2,求DN+MN的最小值;(注:计算时可使用如下定理:在直角△ABC中,若∠C=90°,则AB2=AC2+BC2)
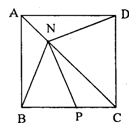
(Ⅲ)若点P在射线BC上,且NB=NP,求证:NP⊥ND。
|
解:(Ⅰ)∵E、F为AC的三等分点, |
  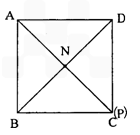 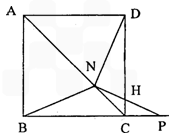 |

如图,把两个全等的腰长为8的等腰直角三角形沿他们的斜边拼接得到四边形ABCD,N是斜边AC上一动点.
(Ⅰ)若E、F为AC的三等分点,求证:∠ADE=∠CBF;
|
(Ⅱ)若M是DC上一点,且DM=2,求DN+MN的最小值;
(注:计算时可使用如下定理:在直角△ABC中,若∠C=90°,则AB2=AC2+BC2.)
|
(Ⅲ)若点P在射线BC上,且NB=NP,求证:NP⊥ND.
 AC,CF=
AC,CF= AC
AC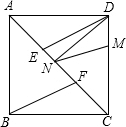 动点.
动点.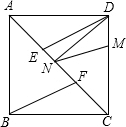 动点.
动点.
