题目内容
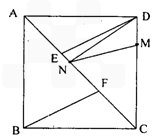
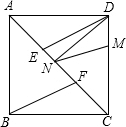
如图,把两个全等的腰长为8的等腰直角三角形沿他们的斜边拼接得到四边形ABCD,N是斜边AC上一动点.
(Ⅰ)若E、F为AC的三等分点,求证:∠ADE=∠CBF;
|
(Ⅱ)若M是DC上一点,且DM=2,求DN+MN的最小值;
(注:计算时可使用如下定理:在直角△ABC中,若∠C=90°,则AB2=AC2+BC2.)
|
(Ⅲ)若点P在射线BC上,且NB=NP,求证:NP⊥ND.
(Ⅰ)证明:∵E、F为AC的三等分点,
|
∵AB=BC,∠ABC=90°,
∵∠BAC=∠BCA=45°.
同理∠DAC=45°.
∴∠BCA=∠DAC.
∵△ASC≌△CDA,
∴CB=AD.
∴在△ADE和△CBF中,
![]() AE=CF,
AE=CF,
∠DAE=∠BCF,
AD=CB,
∴△ADE≌△CBF(SAS).
∴∠ADE=∠CBF.
(Ⅱ)∵D、B关于AC对称,所以当B、N、M在一直线上时,DN+MN最小.
∵AB=8,DM=2,∴CM=6.
在Rt△MCB中,∠MCB=90°,CM=6,BC=8,根据题中定理可求出BM=10.
∴DN+MN最小值为10.
(Ⅲ)①当点P在线段BC上(P与B、C不重合)时,
∵NB=NP, ∴∠NBP=∠NPB.
∵D、B关于AC对称,
∴∠NBP=∠NDC.
∴∠NPB+∠NPC=∠NDC+∠NPC=180°.
∴∠DNP=360°-(∠BCD+∠NDC+∠NPC)=90°.
∴NP⊥ND. ②当点P与点C重合时,点N恰好在AC的中点处,
∵∠NDC=∠NCD=45°,∴∠DNC=90°.
∴NP⊥ND.
③当点P在BC延长线上时,
∵NB=NP,∴∠NBP=∠NPB.
∴D、B关于AC对称,∠NBP=∠NDC.
∴∠NPC=∠NDC.∵∠DHN=∠CHP,
∴∠DNP=∠DCP=90°.∴NP⊥ND.
|
|
| |

 名校课堂系列答案
名校课堂系列答案





 动点.
动点.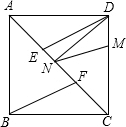 动点.
动点.