题目内容
3.已知关于x的方程ax2+bx+c=0(a>0,b>0)有两个不相等的实数根,则抛物线y=ax2+bx+c的顶点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 由抛物线的解析式可求出顶点的横纵坐标,结合已知条件即可判断抛物线y=ax2+bx+c的顶点所在象限.
解答 解:∵关于x的方程ax2+bx+c=0(a>0,b>0)有两个不相等的实数根,
∴b2-4ac>0,
即b2>4ac,
∵顶点的横坐标为-$\frac{b}{2a}$,纵坐标为$\frac{4ac-{b}^{2}}{4a}$,a>0,b>0,
∴-$\frac{b}{2a}$<0,$\frac{4ac-{b}^{2}}{4a}$<0,
∴抛物线y=ax2+bx+c的顶点在第三象限,
故选C.
点评 此题主要考查了抛物线与一元二次方程的关系,解题的关键是掌握一元二次方程根的判别式和二次函数的顶点坐标公式.

练习册系列答案
相关题目
18.某树苗培育基地培育了1000棵银杏树苗,为了解树苗的长势,测量了6棵树苗的高(单位:cm),其分别为51,48,51,49,52,49,则这1000棵树苗的方差的估计值为( )
| A. | 1 | B. | 1.5 | C. | 2 | D. | 3 |
13.已知a与1的和是一个负数,则|a|=( )
| A. | a | B. | -a | C. | a或-a | D. | 无法确定 |
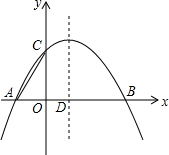 已知二次函数y=ax2+bx+c的图象经过A(-2,0)、B(4,0)、C(O,3)三点,连接AC,该二次函数图象的对称轴与x轴相交于点D.
已知二次函数y=ax2+bx+c的图象经过A(-2,0)、B(4,0)、C(O,3)三点,连接AC,该二次函数图象的对称轴与x轴相交于点D. 如图,平面内有四个点A,B,C,D.
如图,平面内有四个点A,B,C,D. 按要求完成下列各小题.
按要求完成下列各小题.