题目内容
 12、如图,已知AB=BE,BC=BD,∠1=∠2,那么图中
12、如图,已知AB=BE,BC=BD,∠1=∠2,那么图中△ABC
≌△EBD
,AC=ED
,∠ABC=∠EBD
.分析:在等式∠1=∠2两边都加上∠ABD,得到∠ABC与∠EBD相等,然后利用“SAS”得到△ABC与△EBD全等,根据全等三角形的对应表相等得到AC与ED相等.
解答:解:∵∠1=∠2,
∴∠1+∠ABD=∠2+∠ABD,即∠ABC=∠EBD,
在△ABC和△EBD中,
AB=EB,∠ABC=∠EBD,BD=BC,
∴△ABC≌△EBD,
∴AC=ED.
故答案为:△EBD、△ABC;ED;∠EBD.
∴∠1+∠ABD=∠2+∠ABD,即∠ABC=∠EBD,
在△ABC和△EBD中,
AB=EB,∠ABC=∠EBD,BD=BC,
∴△ABC≌△EBD,
∴AC=ED.
故答案为:△EBD、△ABC;ED;∠EBD.
点评:此题考查了全等三角形的性质与判定.由已知的∠1=∠2,利用等式的性质推出∠ABC=∠EBD是本题的突破点.
其中全等三角形的判别方法有:SAS;SSS;ASA;AAS及HL,应根据题中的条件灵活选择合适的方法.
其中全等三角形的判别方法有:SAS;SSS;ASA;AAS及HL,应根据题中的条件灵活选择合适的方法.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 22、如图,已知AB=DF,BE=FC,∠B=∠F.求证:AC=DE.
22、如图,已知AB=DF,BE=FC,∠B=∠F.求证:AC=DE. 如图:已知AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,连接AD并延长,与BC相交于点E.
如图:已知AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,连接AD并延长,与BC相交于点E.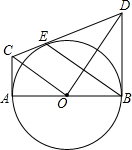 如图,已知AB是⊙O的直径,CA,DB分别与⊙O相切于点A,B,E为上⊙O的一点,连接CE并延长交BD于点D,连接OC,BE,OC∥BE.若AB=3,AC=1,BD=
如图,已知AB是⊙O的直径,CA,DB分别与⊙O相切于点A,B,E为上⊙O的一点,连接CE并延长交BD于点D,连接OC,BE,OC∥BE.若AB=3,AC=1,BD= 如图,已知AB=BE,BC=BD,∠1=∠2,那么图中________≌________,AC=________,∠ABC=________.
如图,已知AB=BE,BC=BD,∠1=∠2,那么图中________≌________,AC=________,∠ABC=________.