题目内容
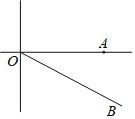
【题目】点![]() 是
是![]() 轴正半轴的一个动点,过点
轴正半轴的一个动点,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交双曲线
交双曲线![]() 于点
于点![]() ,连接
,连接![]() .
.
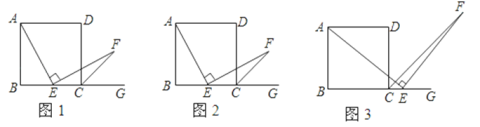
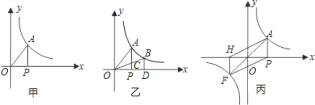
![]() 如图甲,当点
如图甲,当点![]() 在
在![]() 轴的正方向上运动时,
轴的正方向上运动时,![]() 的面积大小是否变化?若不变,请求出
的面积大小是否变化?若不变,请求出![]() 的面积;若改变,试说明理由;
的面积;若改变,试说明理由;
![]() 如图乙,在
如图乙,在![]() 轴上的点
轴上的点![]() 的右侧有一点
的右侧有一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线交双曲线于点
轴的垂线交双曲线于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,设
,设![]() 的面积是
的面积是![]() ,梯形
,梯形![]() 的面积为
的面积为![]() ,写出
,写出![]() 与
与![]() 的大小关系(用 “
的大小关系(用 “![]() ”、“
”、“![]() ”、“
”、“![]() ”表示);
”表示);
![]() 如图丙,
如图丙,![]() 的延长线与双曲线
的延长线与双曲线![]() 的另一个交点为
的另一个交点为![]() ,
,![]() 垂直于
垂直于![]() 轴,垂足为点
轴,垂足为点![]() ,连接
,连接![]() ,
,![]() ,试证明四边形
,试证明四边形![]() 的面积为一个常数.
的面积为一个常数.
【答案】(1)![]() 的面积不变,
的面积不变,![]() ;
; ![]() ;
; ![]() 四边形
四边形![]() 的面积是
的面积是![]() .
.
【解析】
(1)本题还可依据比例系数k的几何意义,得出两个三角形的面积都等于![]() ,因而当点P在x轴的正方向上运动时,Rt△AOP的面积大小不变;
,因而当点P在x轴的正方向上运动时,Rt△AOP的面积大小不变;
(2)根据(1)可以得到△BDO的面积,因而S1>S2;
(3)设A的坐标是(a,b),根据反比例函数是中心对称图形,因而F点的坐标是(-a,-b),则AP=b,HP=2a,则四边形APFH的面积是2ab,从而得到四边形APFH的面积是2.
(1)![]() 的面积不变,
的面积不变,![]() ;
;
![]() 根据
根据![]() 的面积等于
的面积等于![]() ,
,![]() 的面积大于
的面积大于![]() ,
,![]() ;
;
![]() 设
设![]() 的坐标是
的坐标是![]() ,根据反比例函数是中心对称图形,因而
,根据反比例函数是中心对称图形,因而![]() 点的坐标是
点的坐标是![]() ,则
,则![]() ,
,![]() ,则四边形
,则四边形![]() 的面积是
的面积是![]() ,据
,据![]() 在双曲线
在双曲线![]() 的图象上,因而
的图象上,因而![]() ,则四边形
,则四边形![]() 的面积是
的面积是![]() .
.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
【题目】某公司欲招聘一名部门经理,对甲、乙、丙三名候选人进行了笔试与面试,甲、乙、丙三人的笔试成绩分别为95分、94分和94分.他们的面试成绩如表:
候选人 | 评委1 | 评委2 | 评委3 |
甲 | 94 | 89 | 90 |
乙 | 92 | 90 | 94 |
丙 | 91 | 88 | 94 |
(1)分别求出甲、乙、丙三人的面试成绩的平均分![]() 、
、![]() 、和
、和![]() ;
;
(2)若按笔试成绩的40%与面试成绩的60%的和作为综合成绩,综合成绩高者将被录用,请你通过计算判断谁将被录用.