Question

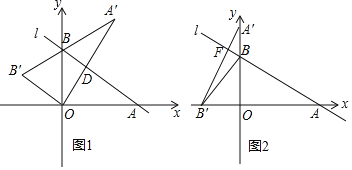
【题目】如图1，在平面直角坐标系中，直线l与坐标轴相交于A（2，0），B（0，）两点，将Rt△AOB绕原点O逆时针旋转到Rt△A′OB′．

（1）求直线l的解析式；

（2）若OA′⊥AB，垂足为D，求点D的坐标；

（3）如图2，若将Rt△AOB绕原点O逆时针旋转90°，A′B′与直线l相交于点F，点E为x轴上一动点，试探究：是否存在点E，使得以点A，E，F为顶点的三角形和△A′BB′相似，若存在，请求出点E的坐标，若不存在，请说明理由．

Answer 1

【答案】（1）直线l的解析式为y＝﹣x+；（2）D（，）；（3）存在，E坐标为（，0）或（﹣4，0）．

【解析】

（1）利用待定系数法即可解决问题．
（2）根据两直线垂直k的乘积为-1，求出直线OA′的解析式，在构建方程组求出交点D坐标．
（3）利用方程组求出答为F坐标，分两种情形分别求解即可解决问题．

解：（1）设直线l的解析式为y＝kx+b，则有，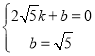

∴，

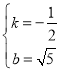∴直线l的解析式为y＝﹣x+；

（2）∵OA′⊥AB，直线AB的解析式为y＝﹣x+，

∴直线OA′的解析式为y＝2x，

，

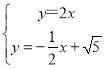解得，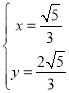

∴D（，）．

（3）如图2中，设E（m，0），

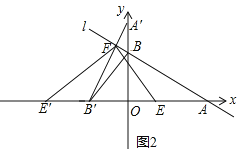
由题意直线A′B′的解析式为y＝2x+2，

由，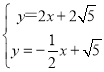

，解得，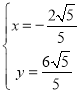

∴F（，）

∵A′（0，2），B′（﹣，0），A（2，0），

∴A′B＝，A′B′＝5，AF＝6，

∵∠FAO＝∠B′A′B，

∴当时，△EAF∽△BA′B′，

即，

∴m＝，

∴E（，0）．

当时，△EAF∽△B′A′B，

即=，

∴m＝﹣4，

∴E（﹣4，0），

综上所述，满足条件的点E坐标为（，0）或（﹣4，0）．