Question

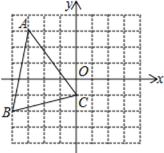
【题目】如图，在平面直角坐标系中，抛物线经过点，顶点为点，点为抛物线上的一个动点，是过点且垂直于轴的直线，过作，垂足为，连接．

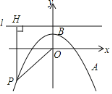
求抛物线的解析式，并写出其顶点的坐标；

①当点运动到点处时，计算：________，________，由此发现，________（填“”、“”或“”）；

②当点在抛物线上运动时，猜想与有什么数量关系，并证明你的猜想．

Answer 1

【答案】(1) y=x2+1,顶点B(0,1); (2)，，;②见解析;

【解析】

（1）利用待定系数法，把点A（4，-3）代入抛物线的解析式，即可解决问题．
（2）①求出PO、PH的长，即可解决问题．
②结论：PO=PH．设点P坐标（m，-m2+1），利用两点之间距离公式求出PH、PO即可解决问题．

(1)∵抛物线y=ax +1经过点A(4,3)，

∴3=16a+1,

∴a=，

∴抛物线解析式为y=x+1,顶点B(0,1).

(2)①当P点运动到A点处时,∵PO==5,PH=2(3)=5，

∴PO=PH，

故答案分别为5，5，=.

②结论：．
理由：设点坐标，
∵
，
∴．