题目内容
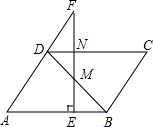
如图，在△ABC中，AB=AC，D点在AB上，DE⊥AC于E，EF⊥BC于F．若∠BDE=140°，那么∠DEF等于（ ）
| A．70° | B．65° | C．60° | D．55° |
∵∠BDE=140°，
∴∠ADE=180°-∠BDE=40°，
∵DE⊥AC，
∴∠AED=90°，
∴∠A=180°-∠AED=∠ADE=50°，
∵AB=AC，
∴∠B=∠C=
（180°-∠A）=65°，
∵EF⊥BC，
∴∠EFC=90°，
∴∠FEC=180°-∠C-∠EFC=25°，
∴∠DEF=180°-90°-25°=65°．
故选B．
∴∠ADE=180°-∠BDE=40°，
∵DE⊥AC，
∴∠AED=90°，
∴∠A=180°-∠AED=∠ADE=50°，
∵AB=AC，
∴∠B=∠C=
| 1 |
| 2 |
∵EF⊥BC，
∴∠EFC=90°，
∴∠FEC=180°-∠C-∠EFC=25°，
∴∠DEF=180°-90°-25°=65°．
故选B．
练习册系列答案
相关题目
