题目内容
 如图,反比例函数
如图,反比例函数 (k>0)与一次函数
(k>0)与一次函数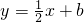 的图象相交于两点A(x1,y1),B(x2,y2),线段AB交y轴与C,当|x1-x2|=2且AC=2BC时,k、b的值分别为
的图象相交于两点A(x1,y1),B(x2,y2),线段AB交y轴与C,当|x1-x2|=2且AC=2BC时,k、b的值分别为
- A.k=
 ,b=2
,b=2 - B.k=
 ,b=1
,b=1 - C.k=
 ,b=
,b=
- D.k=
 ,b=
,b=
D
分析:首先由AC=2BC,可得出A点的横坐标的绝对值是B点横坐标绝对值的两倍.再由|x1-x2|=2,可求出A点与B点的横坐标,然后根据点A、点B既在一次函数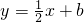 的图象上,又在反比例函数
的图象上,又在反比例函数 (k>0)的图象上,可求出k、b的值.
(k>0)的图象上,可求出k、b的值.
解答:∵AC=2BC,
∴A点的横坐标的绝对值是B点横坐标绝对值的两倍.
∵点A、点B都在一次函数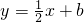 的图象上,
的图象上,
∴可设B(m, m+b),则A(-2m,-m+b).
m+b),则A(-2m,-m+b).
∵|x1-x2|=2,
∴m-(-2m)=2,
∴m= .
.
又∵点A、点B都在反比例函数 (k>0)的图象上,
(k>0)的图象上,
∴ (
( +b)=(-
+b)=(- )(-
)(- +b),
+b),
∴b= ;
;
∴k= (
( +
+ )=
)= .
.
故选D.
点评:此题综合考查了反比例函数、一次函数的性质,注意通过解方程组求出k、b的值.此题难度稍大,综合性比较强,注意对各个知识点的灵活应用.
分析:首先由AC=2BC,可得出A点的横坐标的绝对值是B点横坐标绝对值的两倍.再由|x1-x2|=2,可求出A点与B点的横坐标,然后根据点A、点B既在一次函数
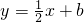 的图象上,又在反比例函数
的图象上,又在反比例函数 (k>0)的图象上,可求出k、b的值.
(k>0)的图象上,可求出k、b的值.解答:∵AC=2BC,
∴A点的横坐标的绝对值是B点横坐标绝对值的两倍.
∵点A、点B都在一次函数
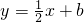 的图象上,
的图象上,∴可设B(m,
 m+b),则A(-2m,-m+b).
m+b),则A(-2m,-m+b).∵|x1-x2|=2,
∴m-(-2m)=2,
∴m=
 .
.又∵点A、点B都在反比例函数
 (k>0)的图象上,
(k>0)的图象上,∴
 (
( +b)=(-
+b)=(- )(-
)(- +b),
+b),∴b=
 ;
;∴k=
 (
( +
+ )=
)= .
.故选D.
点评:此题综合考查了反比例函数、一次函数的性质,注意通过解方程组求出k、b的值.此题难度稍大,综合性比较强,注意对各个知识点的灵活应用.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 如图,反比例函数y=
如图,反比例函数y= 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数 如图,反比例函数
如图,反比例函数