题目内容
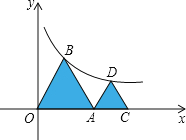
【题目】如图,△OAB和△ACD是等边三角形,O、A、C在x轴上,B、D在y=![]() (x>0)的图象上,则点C的坐标是( )
(x>0)的图象上,则点C的坐标是( )
A.(﹣1+![]() ,0) B.(1+
,0) B.(1+![]() ,0) C.(2
,0) C.(2![]() ,0) D.(2+
,0) D.(2+![]() ,0)
,0)
【答案】C
【解析】
试题分析:设△OAB,△ACD边长的为a,b,根据等边三角形的性质可得点B的纵坐标,点D的纵坐标,代入反比例函数解析式可得两个等边三角形边长,即可求点C的坐标.
解:如图,分别过点B,D作x轴的垂线,垂足分别为E,F.设△OAB,△ACD边长的为a,b,则BE=![]() a,DF=
a,DF=![]() b,
b,
∴点B,D的坐标为(![]() a,
a,![]() a),(a+
a),(a+![]() b,
b,![]() b),
b),
∵点B、D在函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴![]() a×
a×![]() a=(a+
a=(a+![]() b)×
b)×![]() b=
b=![]() ,
,
解得a=2,b=2![]() ﹣2.
﹣2.
∴OC=a+b=2+2![]() ﹣2=2
﹣2=2![]() ,
,
∴C(2![]() ,0).
,0).
故选C.


练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目