题目内容
3.如图,我们可以用“三角形面积等于水平宽(a)与铅垂高(h)乘积的一半”的方法来计算三角形面积.已知开口向下的抛物线y=ax2+bx+c交x轴于A(-1,0)、B(5,0)两点,交y轴于点C(0,5)(1)求抛物线的解析式;
(2)写出该抛物线的对称轴及顶点M的坐标;
(3)求△BCM的面积.
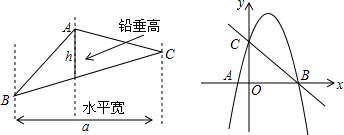
分析 (1)利用A,B,C点坐标结合交点式,求出二次函数解析式即可;
(2)利用配方法求出二次函数对称轴和顶点坐标即可;
(3)利用△BCM的面积=S四边形COBM-S△COB=S四边形CODM+S△MDB-S△COB,进而得出答案.
解答 解:(1)将A,B点代入二次函数解析式可得:
y=a(x+1)(x-5),
再将C(0,5)代入函数解析式得:
5=-5a,
解得:a=-1.
故二次函数解析式为:y=-(x+1)(x-5)=-x2+4x+5;
(2)∵y=-x2+4x+5=-(x-2)2+9,
∴该抛物线的对称轴为:直线x=2,顶点M的坐标为;(2,9);
(3)方法一:如图所示:过点M作MD⊥x轴于点D,
△BCM的面积=S四边形COBM-S△COB
=S四边形CODM+S△MDB-S△COB
=$\frac{1}{2}$(5+9)×2+$\frac{1}{2}$×9×3-$\frac{1}{2}$×5×5
=15.
方法二:设直线BC的解析式为:y=kx+b,
则$\left\{\begin{array}{l}{5k+b=0}\\{b=5}\end{array}\right.$,
解得:k=-1,b=5,
则直线BC的解析式为:y=-x+5,
当x=2时,y=3,
则M到直线BC的铅直高度为:9-3=6,
故△BCM的面积为:$\frac{1}{2}$×5×6=15.
点评 此题主要考查了二次函数的应用以及三角形面积求法和配方法求二次函数顶点坐标,正确分割图形求出其面积是解题关键.

练习册系列答案
相关题目
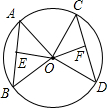 如图,在⊙O中,AB、CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为E、F.
如图,在⊙O中,AB、CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为E、F.