题目内容
如图,已知点P的坐标为(2,1),抛物线y=x2沿OP方向平移,顶点B从O点开始平移到P点结束,设顶点B的横坐标为m.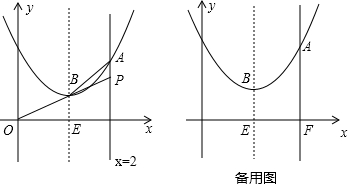
(1)用m的代数式表示点B的坐标;
(2)设直线x=2与抛物线交于点A,与x轴交于点F,平移过程中抛物线的对称轴交x轴于点E.
①当四边形ABEP是平行四边形时,求此时抛物线的解析式;
②探究:当m为何值时,以AB为边的正方形ABCD的顶点C落在坐标轴上?
分析:(1)利用三角形相似,可以求出点B的坐标
(2)利用二次函数平移前后a不变和勾股定理求出.
(2)利用二次函数平移前后a不变和勾股定理求出.
解答:(1)解:在△BOE和△POM中,△BOE∽△POM,
∴
=
,
∵顶点B的横坐标为m,
点P的坐标为(2,1),
∴BE=
,
∴点B的坐标为(m,
);
(2)解:如图1,①∵BE=
,
假设四边形ABEP是平行四边形,
∴AP=BE=
,A(2,1+
),
根据二次函数的顶点坐标为(-
,
),
点B的坐标为(m,
)也是二次函数的顶点坐标,
根据题意得,其中a=1,
解得:b=-2m,c=m2+
,
把点A(2,1+
)代入y=x2+bx+c得;
1+
=4-4m+m2+
,
解得:m=1或3,
∵m≤2,
∴m=1.
∴解析式为:y=x2-2x+
;

②解:以AB为边的正方形ABCD的顶点C落在坐标轴上,分两种情况:
第一种:如图2,C点落在x轴上,如图①.过点A作AG⊥BE于G.
易证△AGB≌△BEC,∴AG=BE,
∴2-m=
,解得m=
;
第二种:如图3,C点落在y轴上,如图②.过点B作GH∥x轴交y轴于G,交PA于H.易证△ABH≌△BCG,∴AH=BG,
∴(2-m)2+
-
=m
解得m=1或4.
∵m≤2,
∴m=1.
综上可知,当m=1或
时,以AB为边的正方形ABCD的顶点C落在坐标轴上.

∴
| OM |
| OE |
| PM |
| BE |
∵顶点B的横坐标为m,
点P的坐标为(2,1),
∴BE=
| m |
| 2 |
∴点B的坐标为(m,
| m |
| 2 |
(2)解:如图1,①∵BE=
| m |
| 2 |
假设四边形ABEP是平行四边形,
∴AP=BE=
| m |
| 2 |
| m |
| 2 |
根据二次函数的顶点坐标为(-
| b |
| 2a |
| 4ac-b2 |
| 4a |
点B的坐标为(m,
| m |
| 2 |
根据题意得,其中a=1,
解得:b=-2m,c=m2+
| m |
| 2 |
把点A(2,1+
| m |
| 2 |
1+
| m |
| 2 |
| m |
| 2 |
解得:m=1或3,
∵m≤2,
∴m=1.
∴解析式为:y=x2-2x+
| 3 |
| 2 |

②解:以AB为边的正方形ABCD的顶点C落在坐标轴上,分两种情况:
第一种:如图2,C点落在x轴上,如图①.过点A作AG⊥BE于G.
易证△AGB≌△BEC,∴AG=BE,
∴2-m=
| m |
| 2 |
| 4 |
| 3 |
第二种:如图3,C点落在y轴上,如图②.过点B作GH∥x轴交y轴于G,交PA于H.易证△ABH≌△BCG,∴AH=BG,
∴(2-m)2+
| m |
| 2 |
| m |
| 2 |
解得m=1或4.
∵m≤2,
∴m=1.
综上可知,当m=1或
| 4 |
| 3 |

点评:此题主要考查了相似三角形的性质,以及二次函数的平移问题,综合性较强.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
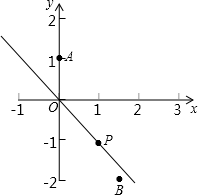 如图,已知点A的坐标为(0,1),点B的坐标为(
如图,已知点A的坐标为(0,1),点B的坐标为(| 3 |
| 2 |
| A、(2,-2) | ||||
| B、(4,-4) | ||||
C、(
| ||||
| D、(5,-5) |
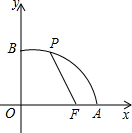 如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-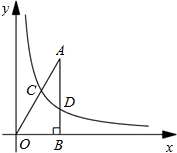 如图,已知点A的坐标为(
如图,已知点A的坐标为(

 如图,已知点A的坐标为(
如图,已知点A的坐标为(