题目内容
如图,在一单位为1的方格纸上,△AA1A2,△A2A3A4,△A4A5A6,△A6A7A8,…,都是一边在x轴上、边长分别为1,2,3,4,…的等边三角形.若△AA1A2的顶点坐标分别为A(0,0),A1( ),A2(1,0),则依如图所示规律,A2013的坐标为( )
),A2(1,0),则依如图所示规律,A2013的坐标为( )
A.(504,0)
B.(
 )
)C.(
 )
)D.(0,-504)
【答案】分析:根据已知图象得出A2013的坐标与A1点的横坐标位置相同,在平行于y轴的直线上,进而得出A点的横纵坐标特点,进而得出答案.
解答:解:由题意可得出A点的坐标变化是4种变化,分别在x轴正半轴和x轴负半轴以及y轴负半轴以及横坐标为 平行于y轴的直线上,
平行于y轴的直线上,
∵2013÷4=503…1,
∴A2013的坐标与A1点的横坐标位置相同,在平行于y轴的直线上,
∵A1( ),△A4A5A6是一边在x轴上,边长为3的等边三角形,
),△A4A5A6是一边在x轴上,边长为3的等边三角形,
∴A5( ,
, ),
),
同理可得出:A9( ,
, )…
)…
∴A2013的横坐标为: ,
,
∵5=1×4+1,9=2×4+1,13=3×4+1,…
∴2013=503×4+1,
其纵坐标分母为2,分子是连续奇数与 的积,
的积,
∴A2013是与A1点的横坐标相同,且在平行于y轴的直线上的第504个数据,
A2013的纵坐标为: =
= ,
,
∴A2013的坐坐标为:( ,
, ).
).
故选B.
点评:此题主要考查了点的规律以及勾股定理和等边三角形的性质等知识,根据已知得出点的变化规律是解题关键.
解答:解:由题意可得出A点的坐标变化是4种变化,分别在x轴正半轴和x轴负半轴以及y轴负半轴以及横坐标为
 平行于y轴的直线上,
平行于y轴的直线上,∵2013÷4=503…1,
∴A2013的坐标与A1点的横坐标位置相同,在平行于y轴的直线上,
∵A1(
 ),△A4A5A6是一边在x轴上,边长为3的等边三角形,
),△A4A5A6是一边在x轴上,边长为3的等边三角形,∴A5(
 ,
, ),
),同理可得出:A9(
 ,
, )…
)…∴A2013的横坐标为:
 ,
,∵5=1×4+1,9=2×4+1,13=3×4+1,…
∴2013=503×4+1,
其纵坐标分母为2,分子是连续奇数与
 的积,
的积,∴A2013是与A1点的横坐标相同,且在平行于y轴的直线上的第504个数据,
A2013的纵坐标为:
 =
= ,
,∴A2013的坐坐标为:(
 ,
, ).
).故选B.
点评:此题主要考查了点的规律以及勾股定理和等边三角形的性质等知识,根据已知得出点的变化规律是解题关键.

练习册系列答案
相关题目
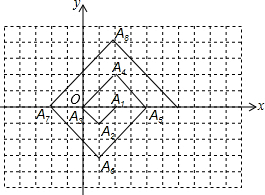 如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2014的坐标为( )
如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2014的坐标为( )| A、(2,1008) | B、(1,-1007) | C、(-1008,0) | D、(1008,0) |
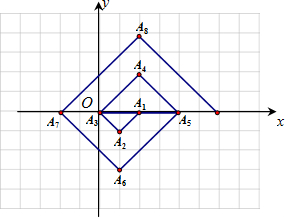 (2012•德州)如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2012的坐标为
(2012•德州)如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2012的坐标为 (2013•历城区二模)如图,在一单位为1的方格纸上,△AA1A2,△A2A3A4,△A4A5A6,△A6A7A8,…,都是一边在x轴上、边长分别为1,2,3,4,…的等边三角形.若△AA1A2的顶点坐标分别为A(0,0),A1(
(2013•历城区二模)如图,在一单位为1的方格纸上,△AA1A2,△A2A3A4,△A4A5A6,△A6A7A8,…,都是一边在x轴上、边长分别为1,2,3,4,…的等边三角形.若△AA1A2的顶点坐标分别为A(0,0),A1( 如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7…,都是斜边在x轴上,斜边长分别为2,4,6,…的等腰直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2012的坐标为( )
如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7…,都是斜边在x轴上,斜边长分别为2,4,6,…的等腰直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2012的坐标为( )