题目内容
如图(1),在地面A、B两处测得地面上标杆PQ的仰角分别为30°、45°,且测得AB=3米,求标杆PQ的长(2)在数学学习中要注意基本模型的应用,如图(2),是测量不可达物体高度的基本模型:在地面A、B两处测得地面上标杆PQ的仰角分别为α、β,且测得AB=a米.
设PQ=h米,由PA-PB=a可得关于h的方程
| atanβ•tanα | tanβ-tanα |
(3)请用上述基本模型解决下列问题:如图3,斜坡AP的倾斜角为15°,在A处测得Q的仰角为45°,要测量斜坡上标杆PQ的高度,沿着斜坡向上走10米到达B,在B处测得Q的仰角为60°,求标杆PQ的高.(结果可含三角函数)
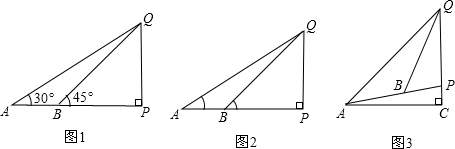
分析:(1)设标杆PQ长为x米,在RT△PAQ中求出AP,在RT△PBQ中求出BP,然后根据PA-PB=AB得出方程,解出即可.
(2)分别表示出PA、PB,然后代入PA-PB=a即可得出答案.
(3)过点Q作QD⊥AP于点D,根据图形中的三角函数关系可表示出QD,继而RT△QPD中可表示出PQ.
(2)分别表示出PA、PB,然后代入PA-PB=a即可得出答案.
(3)过点Q作QD⊥AP于点D,根据图形中的三角函数关系可表示出QD,继而RT△QPD中可表示出PQ.
解答:解:(1)如图1,设标杆PQ长为x米,
在RT△PAQ中,AP=
=
x,
在RT△PBQ中,BP=
=x
由PA-PB=AB,得
x-x=3,
解得x=
≈4.1(3分)答:标杆PQ的长约为4.1;
(2)PA=
,PB=
,
∴可得
-
=a;
(3)过点Q作QD⊥AP于点D,

∠QAP=30°,∠QBP=45°,AB=10米,由(2)得,QD=
在RT△QPD中,∠QPD=75°,
PQ=
=
=
.
在RT△PAQ中,AP=
| PQ |
| tan30° |
| 3 |
在RT△PBQ中,BP=
| PQ |
| tan45° |
由PA-PB=AB,得
| 3 |
解得x=
3
| ||
| 2 |
(2)PA=
| h |
| tanα |
| h |
| tanβ |
∴可得
| h |
| tanα |
| h |
| tanβ |
(3)过点Q作QD⊥AP于点D,

∠QAP=30°,∠QBP=45°,AB=10米,由(2)得,QD=
| 10tan30°•tan45° |
| tan45°-tan30° |
在RT△QPD中,∠QPD=75°,
PQ=
| QD |
| sin75° |
| 10tan30°•tan45° |
| sin75°(tan45°-tan30°) |
10
| ||
sin75°•(3-
|
点评:本题考查解直角三角形的应用,难度较大,解答本题的关键是掌握各三角函数在直角三角形中的表示形式.

练习册系列答案
相关题目
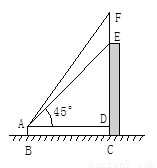
 20、如图,王明站在地面B处用测角仪器测得楼顶点E的仰角为45°,楼顶上旗杆顶点F的仰角为55°,已知测角仪器高AB=1.5米,楼高CE=14.5米,求旗杆EF的高度(精确到1米).(供参考数据:sin55°≈0.8,cos55°≈0.57,tan55°≈1.4.)
20、如图,王明站在地面B处用测角仪器测得楼顶点E的仰角为45°,楼顶上旗杆顶点F的仰角为55°,已知测角仪器高AB=1.5米,楼高CE=14.5米,求旗杆EF的高度(精确到1米).(供参考数据:sin55°≈0.8,cos55°≈0.57,tan55°≈1.4.)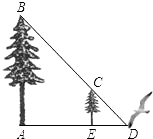 如图,小鸟的妈妈在地面D处寻找到食物,准备飞到大树的顶端B处给非常饥饿的小鸟喂食,途中经过小树树顶C处,已知小树高为4米,大树与小树之间的距离为9米,已知tan∠BDA=
如图,小鸟的妈妈在地面D处寻找到食物,准备飞到大树的顶端B处给非常饥饿的小鸟喂食,途中经过小树树顶C处,已知小树高为4米,大树与小树之间的距离为9米,已知tan∠BDA=