题目内容
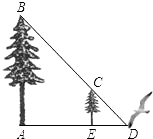如图，小鸟的妈妈在地面D处寻找到食物，准备飞到大树的顶端B处给非常饥饿的小鸟喂食，途中经过小树树顶C处，已知小树高为4米，大树与小树之间的距离为9米，已知tan∠BDA=| 4 | 3 |
分析：已知tan∠BDA=
，小树高为4米，即CE=4米，就可以求出ED的长，根据CE∥AB，得到
=
就可以求出AB，在直角△ABD中，根据勾股定理就可以得到BD的长．
| 4 |
| 3 |
| CE |
| AB |
| CE |
| AD |
解答：解法一：∵CE⊥AD，BA⊥AD，
∴△BAD和△CED都是Rt△，
又tan∠BDA=
，
∴
=
，
又CE=4米，
∴ED=3米，
又AD=AE+ED=12米，CE⊥AD，AB⊥AD，
∴CE∥AB，
∴
=
，
又CE=4米，ED=3米，AE=9米，
∴AB=16米，
∴BD=
=20米．
答：小鸟妈妈至少飞行20米；
解法二：∵CE⊥AD，
∴△CED为Rt△，
由tan∠BDA=
，CE=4，
∴ED=3米，
又CD=
=
=5，
又AB⊥AD，∴CE∥AB，
∴
=
?BD=
=
=20米．
答：小鸟妈妈至少飞行20米．
∴△BAD和△CED都是Rt△，
又tan∠BDA=
| 4 |
| 3 |
∴
| CE |
| ED |
| 4 |
| 3 |
又CE=4米，
∴ED=3米，
又AD=AE+ED=12米，CE⊥AD，AB⊥AD，
∴CE∥AB，
∴
| CE |
| AB |
| CE |
| AD |
又CE=4米，ED=3米，AE=9米，
∴AB=16米，
∴BD=
| AB2+AD2 |
答：小鸟妈妈至少飞行20米；
解法二：∵CE⊥AD，
∴△CED为Rt△，
由tan∠BDA=
| 4 |
| 3 |
∴ED=3米，
又CD=
| CE2+ED2 |
| 32+42 |
又AB⊥AD，∴CE∥AB，
∴
| CD |
| BD |
| ED |
| AD |
| CD×AD |
| ED |
| 5(9+3) |
| 3 |
答：小鸟妈妈至少飞行20米．
点评：此题首先要正确理解题意，把实际问题转化成三角函数的问题，然后利用三角函数解决问题．
练习册系列答案
阅读快车系列答案
相关题目
，问小鸟妈妈从D处飞到B处至少要飞行多少米？（D、C、B三点共线）
，问小鸟妈妈从D处飞到B处至少要飞行多少米？（D、C、B三点共线）
，问小鸟妈妈从D处飞到B处至少要飞行多少米？（D、C、B三点共线）