题目内容
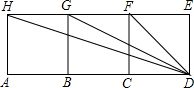
 如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形,图中与△HBC相似的三角形为( )
如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形,图中与△HBC相似的三角形为( )分析:设正方形ABGH的边长为1,先运用勾股定理分别求出HB、HC的长,将其三边按照从大到小的顺序求出比值,再分别求出四个选项中每一个三角形三边的比值,根据三组对应边的比相等的两个三角形相似求解即可.
解答:解:设正方形ABGH的边长为1,运用勾股定理得HB=
,HC=
,则HC:HB:BC=
:
:1.
A、∵HB=
,BD=2,HD=
,∴HD:BD:HB=
:2:
=
:
:1,∴HC:HB:BC=HD:BD:HB,∴△HBC∽△DBH,故本选项正确;
B、∵HC=
,CD=1,HD=
,∴HD:HC:CD=
:
:1,∴HC:HB:BC≠HD:HC:CD,∴△HBC与△HCD不相似,故本选项错误;
C、∵HA=1,AC=2,HC=
,HC:AC:HA=
:2:1,∴HC:HB:BC≠HC:AC:HA,∴△HBC与△HAC不相似,故本选项错误;
D、∵HA=1,AD=3,HD=
,HD:AD:HA=
:3:1,∴HC:HB:BC≠HD:AD:HA,∴△HBC与△HAD不相似,故本选项错误.
故选A.
| 2 |
| 5 |
| 5 |
| 2 |
A、∵HB=
| 2 |
| 10 |
| 10 |
| 2 |
| 5 |
| 2 |
B、∵HC=
| 5 |
| 10 |
| 10 |
| 5 |
C、∵HA=1,AC=2,HC=
| 5 |
| 5 |
D、∵HA=1,AD=3,HD=
| 10 |
| 10 |
故选A.
点评:本题考查了相似三角形的判定,判定两个三角形相似的一般方法有:(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;
(2)三边法:三组对应边的比相等的两个三角形相似;
(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;
(4)两角法:有两组角对应相等的两个三角形相似.
本题还可以利用方法(3)进行判定.
(2)三边法:三组对应边的比相等的两个三角形相似;
(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;
(4)两角法:有两组角对应相等的两个三角形相似.
本题还可以利用方法(3)进行判定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
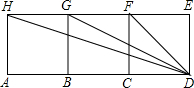 如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形.请从图中找出二对相似三角形,要求其中一对必须不是直角三角形,并说明这一对三角形相似的理由.
如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形.请从图中找出二对相似三角形,要求其中一对必须不是直角三角形,并说明这一对三角形相似的理由. 如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形.则∠ACH+∠ADH的值为( )
如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形.则∠ACH+∠ADH的值为( )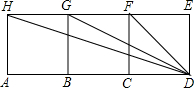 如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形.请从图中找出二对相似三角形,要求其中一对必须不是直角三角形,并说明这一对三角形相似的理由.
如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形.请从图中找出二对相似三角形,要求其中一对必须不是直角三角形,并说明这一对三角形相似的理由.