题目内容
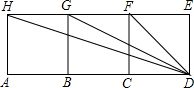
 如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形.则∠ACH+∠ADH的值为( )
如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形.则∠ACH+∠ADH的值为( )分析:由四边形ABGH,四边形BCFG,四边形CDEF都是正方形,易得
=
=
,继而可证得△HBC∽△DBH,然后有相似三角形对应角相等,求得∠ACH=∠DHB,再利用三角形外角的性质求解即可求得答案.
| BC |
| BH |
| BH |
| BD |
| 1 | ||
|
解答:解:∵四边形ABGH,四边形BCFG,四边形CDEF都是正方形,设边长为a,
则BH=
=
a,BC=a,BD=2a,
∴
=
=
,
又∵∠HBC=∠DBH(公共角),
∴△HBC∽△DBH,
∴∠ACH=∠DHB,
∴∠ACH+∠ADH=∠DHB+∠ADH=∠ABH=45°.
故选A.
则BH=
| AB2+AH2 |
| 2 |
∴
| BC |
| BH |
| BH |
| BD |
| 1 | ||
|
又∵∠HBC=∠DBH(公共角),
∴△HBC∽△DBH,
∴∠ACH=∠DHB,
∴∠ACH+∠ADH=∠DHB+∠ADH=∠ABH=45°.
故选A.
点评:此题考查了相似三角形的判定与性质、正方形的性质以及勾股定理.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目
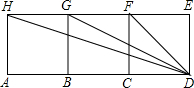 如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形.请从图中找出二对相似三角形,要求其中一对必须不是直角三角形,并说明这一对三角形相似的理由.
如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形.请从图中找出二对相似三角形,要求其中一对必须不是直角三角形,并说明这一对三角形相似的理由. 如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形,图中与△HBC相似的三角形为( )
如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形,图中与△HBC相似的三角形为( )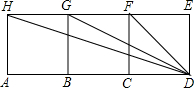 如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形.请从图中找出二对相似三角形,要求其中一对必须不是直角三角形,并说明这一对三角形相似的理由.
如图,四边形ABGH,四边形BCFG,四边形CDEF都是正方形.请从图中找出二对相似三角形,要求其中一对必须不是直角三角形,并说明这一对三角形相似的理由.