题目内容
如图1,一扇窗户打开后用窗钩AB可将其固定.(1)这里所运用的几何原理是( )
(A)三角形的稳定性(B)两点之间线段最短;
(C)两点确定一条直线(D)垂线段最短;
(2)图2是图1中窗子开到一定位置时的平面图,若∠AOB=45°,∠OAB=30°,OA=60cm,求点B到OA边的距离.(
 ≈1.7,结果精确到整数)
≈1.7,结果精确到整数)
【答案】分析:(1)加上窗钩AB后,原图形中具有△AOB了,故这种做法根据的是三角形的稳定性;
(2)点到直线的距离是指点到直线的垂线段的长度,解直角三角形求解即可.
解答: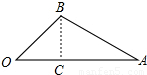 解:(1)A.
解:(1)A.
(2)如图,
过点B作BC⊥OA于点C.
∵∠AOB=45°,
∴∠CBO=45°,BC=OC.
设BC=OC=x,
∵∠OAB=30°,
∴AC=BC×tan60°=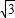 x.
x.
∵OC+CA=OA,
∴x+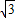 x=60,
x=60,
∴x=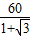 =
=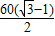 =30
=30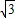 -30≈22(cm).
-30≈22(cm).
即点B到OA边的距离是22cm.
点评:本题考查三角形稳定性的实际应用,三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得.
(2)点到直线的距离是指点到直线的垂线段的长度,解直角三角形求解即可.
解答:
 解:(1)A.
解:(1)A.(2)如图,
过点B作BC⊥OA于点C.
∵∠AOB=45°,
∴∠CBO=45°,BC=OC.
设BC=OC=x,
∵∠OAB=30°,
∴AC=BC×tan60°=
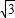 x.
x.∵OC+CA=OA,
∴x+
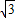 x=60,
x=60,∴x=
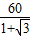 =
=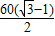 =30
=30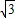 -30≈22(cm).
-30≈22(cm).即点B到OA边的距离是22cm.
点评:本题考查三角形稳定性的实际应用,三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图1,一扇窗户打开后用窗钩AB可将其固定.
(1)这里所运用的几何原理是( )
| A.三角形的稳定性 | B.两点之间线段最短 |
| C.两点确定一条直线 | D.垂线段最短 |
点O到AB边的距离为2cm,求窗钩AB的长(
 ,结果精确到整数)
,结果精确到整数)
 °,∠OAB=30°,OA=60cm,求点B到OA边的距离.(
°,∠OAB=30°,OA=60cm,求点B到OA边的距离.( ,结果精确到整数)
,结果精确到整数)
 ≈1.7,结果精确到整数)
≈1.7,结果精确到整数)
 ≈1.7,结果精确到整数)
≈1.7,结果精确到整数)