题目内容
如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC;OE平分∠BOC.
1.写出图中∠BOD与∠AOE的补角;
2.如果∠COD=25°,那么∠COE=_______;如果∠COD=60°,那么∠COE=________;
3.试猜想∠COD与∠COE具有怎样的数量关系,并说明理由.
1.∠BOD的补角为∠AOD,∠DOC ;
∠AOE的补角为∠BOE,∠EOC. ·························4分
2.65°;30°. ·······························6分
3.∠COD+∠COE=90°. ······································7分
因为OD平分∠AOC,OE平分∠BOC.
所以 ∠COD=![]() ∠AOC , ∠COE=
∠AOC , ∠COE=![]() ∠BOC.
∠BOC.
所以∠COD+∠COE=![]() ∠AOB=
∠AOB=![]()
![]() 180°=90°. ··················10分
180°=90°. ··················10分
解析:略

练习册系列答案
相关题目
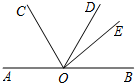 如图,O是直线AB上一点,OC,OD,OE是三条射线,且OC平分∠AOD,∠BOE=2∠DOE,∠COE=80°,求∠BOE的度数.
如图,O是直线AB上一点,OC,OD,OE是三条射线,且OC平分∠AOD,∠BOE=2∠DOE,∠COE=80°,求∠BOE的度数.
 如图,O是直线AB上一点,∠AOC=134°18′,求∠BOC的度数.
如图,O是直线AB上一点,∠AOC=134°18′,求∠BOC的度数. 如图,O是直线AB上的一点,∠AOC=53°17′,则∠BOC的度数是
如图,O是直线AB上的一点,∠AOC=53°17′,则∠BOC的度数是 如图,O是直线AB上任意一点,OC平分∠AOB.按下列要求画图并回答问题:
如图,O是直线AB上任意一点,OC平分∠AOB.按下列要求画图并回答问题: