Question

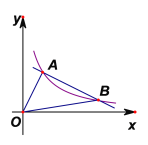
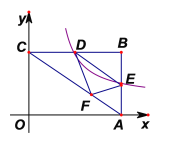
【题目】如图，在平面直角坐标系中，矩形的边、分别在轴和轴上，，，点是边上一动点，过点的反比例函数与边交于点．若将沿折叠，点的对应点恰好落在对角线上． 则反比例函数的解析式是（ ）

A.B.C.D.

Answer 1

【答案】C

【解析】

设,求得DC=,AE=，得到DB=6-,BE=4-,根据三角函数的定义得到tan∠BAC= tan∠BED，根据平行线的判定定理得到DE∥AC,连接BF，根据折叠的性质得到BH=FH，根据平行线分线段成比例得到AE=BE=2，于是得到结论.

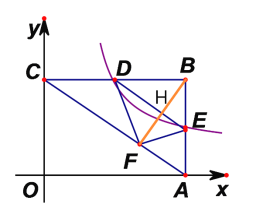
∵四边形OABC是矩形，OA=6,OC=4,

∴BC=OA=6,AB=OC=4,

∴,

设,

∴DC=,AE=,

∴DB=6-,BE=4-,

∴tan∠BED==,

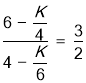∵tan∠BAC=,

∴tan∠BAC= tan∠BED，

∴∠BED=∠BAC,

∴DE∥AC,

连接BF,

∵将△DBE沿DE折叠，点B的对应点F正好落在对角线AC上,

∴BH=FH，

∴AE=BE=2,

∴,

∴k=12.

∴反比例函数的解析式.

故选C.