题目内容
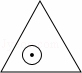
如图,一个半径为1的圆形纸片在边长为a(a≥2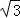 )的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )
)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )
A. 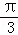 B.
B. 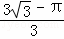
C. 3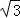 ﹣π D. 不能求出具体值
﹣π D. 不能求出具体值
C
考点: 轨迹.
分析: 过圆形纸片的圆心O1作两边的垂线,垂足分别为D,E,连AO1,则在Rt△ADO1中,可求得AD=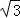 .四边形ADO1E的面积等于三角形ADO1的面积的2倍,还可求出扇形O1DE的面积,所求面积等于四边形ADO1E的面积减去扇形O1DE的面积的三倍.
.四边形ADO1E的面积等于三角形ADO1的面积的2倍,还可求出扇形O1DE的面积,所求面积等于四边形ADO1E的面积减去扇形O1DE的面积的三倍.
解答: 解:如图,当圆形纸片运动到与∠A的两边相切的位置时,
过圆形纸片的圆心O1作两边的垂线,垂足分别为D,E,
连AO1,则Rt△ADO1中,∠O1AD=30°,O1D=1,AD=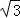 .
.
∴S△ADO1=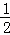 O1D•AD=
O1D•AD=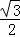 .由S四形形ADO1E=2S△ADO1=
.由S四形形ADO1E=2S△ADO1=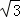 .
.
∵由题意,∠DO1E=120°,得S扇形O1DE=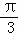 ,
,
∴圆形纸片不能接触到的部分的面积为3(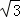 ﹣
﹣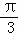 )=3
)=3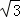 ﹣π.
﹣π.
故选.
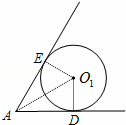

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目


 +(
+( ﹣π)0.
﹣π)0. π
π 的一根为1,求另一根及m的值。
的一根为1,求另一根及m的值。