题目内容
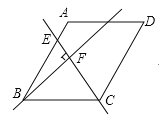
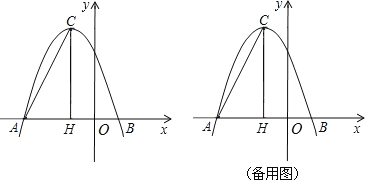
【题目】如图1，在平面直角坐标系xOy中，
与x轴交于A，B两点，与y轴于C，D两点，其中
，
，
．
求圆心M的坐标；
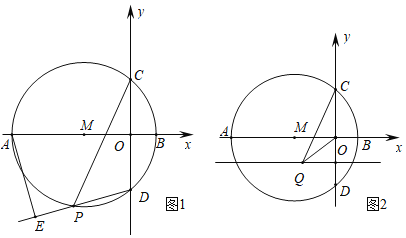
点P为
上任意一点
不与A、D重合
，连接PC，PD，作
的延长线于点
当点P在上运动时，
的值发生变化吗？若不变，求出这个值，若变化，请说明理由．
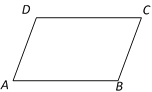
如图2，若点Q为直线
上一个动点，连接QC，QO，当
的值最大时，求点Q的坐标．
【答案】（1）
；（2）
的值不变，理由见解析；（3）点Q坐标为
或
【解析】
利用中点坐标公式计算即可．
结论：
的值不变．如图1中，连接AC，BC，BD，PA，PB，作
于H，在PC上截取一点K，使得
，连接
想办法证明
，
即可解决问题．
如图2中，作线段OC的垂直平分线GF交OC于G，以N为圆心，NC为半径作
，当与直线
相切于点Q时，
的值最大，此时
的值最大．求出HQ的长即可解决问题．
解：
，
，
，
．
结论：的值不变．
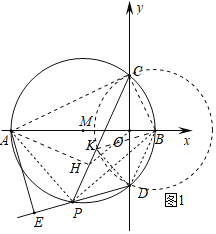
理由：如图1中，连接AC，BC，BD，PA，PB，作于H，在PC上截取一点K，使得，连接BK．
，AB是直径，
，
，
，
，
，
≌
，
，以B为圆心，BC为半径作
，
是
的直径，
，
，
是的切线，
，
，
，H，O，C四点共圆，
，
，
，
，
，
，
，
，
≌
，
，
，
，
，
，
，
，
，
，
，，
，
．
如图2中，作线段OC的垂直平分线GF交OC于G，以N为圆心，NC为半径作，当与直线相切于点Q时，的值最大，此时的值最大．
，
四边形NQHG是矩形，
，
在
中，
，
．
根据对称性可知，当
时，也满足条件．
综上所述．满足条件的点Q坐标为或．
练习册系列答案
相关题目
【题目】抛物线
中，函数值y与自变量
之间的部分对应关系如下表：
| … |
|
|
| 0 | 1 | … |
y | … |
|
| 0 |
|
| … |
（1）求该抛物线的表达式；
（2）如果将该抛物线平移，使它的顶点移到点M（2,4）的位置，那么其平移的方法是____________.
