Question

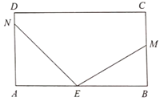
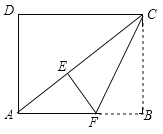
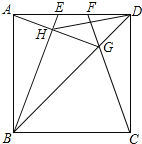
【题目】如图，E、F是正方形ABCD的边AD上的两个动点，满足AE=DF．连接CF交BD于G，连接BE交AG于H．已知正方形ABCD的边长为4cm，解决下列问题：

（1）求证：BE⊥AG；

（2）求线段DH的长度的最小值．

Answer 1

【答案】（1）见解析；(2)2-2．.

【解析】

（1）根据正方形的性质可得AB=AD=CD，∠BAD=∠CDA，∠ADG=∠CDG，然后利用“边角边”证明△ABE和△DCF全等，根据全等三角形对应角相等可得∠1=∠2，利用“边角边”证明△ADG和△CDG全等，根据全等三角形对应角相等可得∠2=∠3，从而得到∠1=∠3，然后求出∠AHB=90°，再根据垂直的定义证明即可；

（2）根据直角三角形斜边上的中线等于斜边的一半，取AB的中点O，连接OH、OD，然后求出OH=AB=2，利用勾股定理列式求出OD，然后根据三角形的三边关系可知当O、D、H三点共线时，DH的长度最小．

（1）证明：在正方形ABCD中，AB=AD=CD，∠BAD=∠CDA，∠ADG=∠CDG，

在△ABE和△DCF中，

，

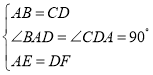∴△ABE≌△DCF（SAS），

∴∠1=∠2，

在△ADG和△CDG中，

，

∴△ADG≌△CDG（SAS），

∴∠2=∠3，

∴∠1=∠3，

∵∠BAH+∠3=∠BAD=90°，

∴∠1+∠BAH=90°，

∴∠AHB=180°-90°=90°，

∴BE⊥AG；

（2）解：如图，取AB的中点O，连接OH、OD，

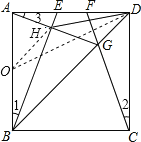
则OH=AO=AB=2，

在Rt△AOD中，OD=，

根据三角形的三边关系，OH+DH＞OD，

∴当O、D、H三点共线时，DH的长度最小，

DH的最小值=OD-OH=2-2．