��Ŀ����
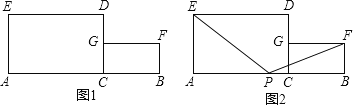
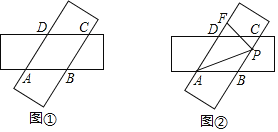
����Ŀ���Ķ�����IJ��ϣ�С������һ�����⣺��ͼ�٣��ڡ�ABC�У�DE//BC�ֱ�AB�ڵ�D����AC�ڵ�E����֪CD![]() BE��CD=2��BE=3����BC+DE��ֵ.
BE��CD=2��BE=3����BC+DE��ֵ.
С�����֣�����E��EF![]() DC����BC���ӳ����ڵ�F�������BEF�����������ͼ����ܹ�ʹ����õ����.
DC����BC���ӳ����ڵ�F�������BEF�����������ͼ����ܹ�ʹ����õ����.
��1���밴������˼·���С�����������⣻
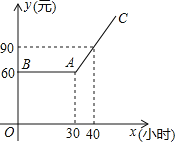
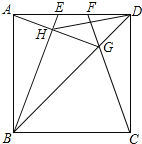
��2���ο�С��˼������ķ����������������⣺��ͼ�ڣ��ı���ABCD��ƽ���ı��Σ��ı���ABEF�Ǿ��Σ�AC��DF���ڵ�G��AC=BF=DF�����DGC�Ķ���.
���𰸡���1��BC+DE=![]() ����2��60����
����2��60����
��������
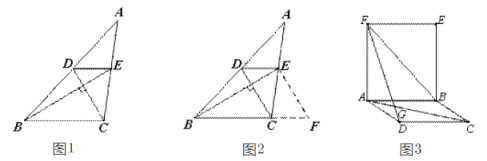
��1����DE��BC��EF��DC����֤���ı���DCFE��ƽ���ı��Σ����ɵ�EF=CD=3��CF=DE�����ɵ�BC+DE=BF��Ȼ�����ù��ɶ��������BC+DE��ֵ��
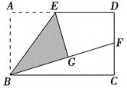
��2����������AE��CE�����ı���ABCD��ƽ���ı��Σ��ı���ABEF�Ǿ��Σ���֤���ı���DCEF��ƽ���ı��Σ��̶�֤�á�ACE�ǵȱ������Σ������ô𰸣�
��1����DE��BC��EF��DC��
���ı���DCFE��ƽ���ı��Σ�
��EF=CD=3��CF=DE��
��CD��BE��
��EF��BE��
��BC+DE=BC+CF=BF=BE2+EF2=![]() ��
��
(2)����AE��CE����ͼ��

���ı���ABCD��ƽ���ı��Σ�
��AB��DC��
���ı���ABEF�Ǿ��Σ�
��AB��FE��BF=AE��
��DC��FE��
���ı���DCEF��ƽ���ı��Σ�
��CE��DF��
��AC=BF=DF��
��AC=AE=CE��
���ACE�ǵȱ������Σ�
���ACE=60����
��CE��DF��
���AGF=��ACE=60����

 ��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
��ĩ���䵥Ԫ�����ิϰ��ϵ�д�