题目内容
如图,抛物线与x轴交于点A(﹣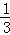 ,0)、点B(2,0),与y轴交于点C(0,1),连接BC.
,0)、点B(2,0),与y轴交于点C(0,1),连接BC.
(1)求抛物线的函数关系式;
(2)点N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(﹣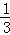 <t<2),求△ABN的面积S与t的函数关系式;
<t<2),求△ABN的面积S与t的函数关系式;
(3)若﹣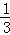 <t<2且t≠0时△OPN∽△COB,求点N的坐标.
<t<2且t≠0时△OPN∽△COB,求点N的坐标.
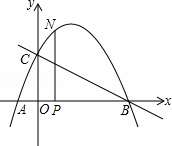
解:(1)设抛物线的解析式为y=ax2+bx+c,由题可得:
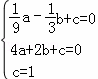 ,
,
解得: ,
,
∴抛物线的函数关系式为y=﹣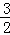 x2+
x2+ x+1;
x+1;
(2)当﹣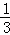 <t<2时,yN>0,
<t<2时,yN>0,
∴NP= =yN=﹣
=yN=﹣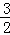 t2+
t2+ t+1,
t+1,
∴S=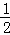 AB•PN
AB•PN
=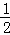 ×(2+
×(2+ )×(﹣
)×(﹣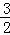 t2+
t2+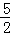 t+1)
t+1)
= (﹣
(﹣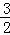 t2+
t2+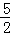 t+1)
t+1)
=﹣ t2+
t2+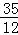 t+
t+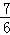 ;
;
(3)∵△OPN∽△COB,
∴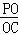 =
=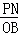 ,
,
∴ =
=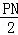 ,
,
∴PN=2PO.
①当﹣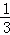 <t<0时,PN=
<t<0时,PN=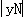 =yN=﹣
=yN=﹣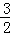 t2+
t2+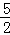 t+1,PO=
t+1,PO= =﹣t,
=﹣t,
∴﹣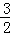 t2+
t2+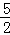 t+1=﹣2t,
t+1=﹣2t,
整理得:3t2﹣9t﹣2=0,
解得:t1=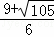 ,t2=
,t2=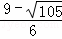 .
.
∵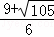 >0,﹣
>0,﹣ <
<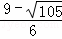 <0,
<0,
∴t=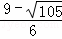 ,此时点N的坐标为(
,此时点N的坐标为(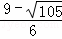 ,
,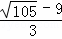 );
);
②当0<t<2时,PN=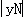 =yN=﹣
=yN=﹣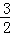 t2+
t2+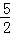 t+1,PO=
t+1,PO= =t,
=t,
∴﹣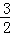 t2+
t2+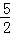 t+1=2t,
t+1=2t,
整理得:3t2﹣t﹣2=0,
解得:t3=﹣ ,t4=1.
,t4=1.
∵﹣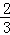 <0,0<1<2,
<0,0<1<2,
∴t=1,此时点N的坐标为(1,2).
综上所述:点N的坐标为( ,
,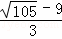 )或(1,2).
)或(1,2).

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
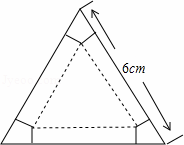
如图,有一块边长为6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
|
| A. |
| B. |
| C. |
| D. |
|
将直尺和直角三角板按如图方式摆放,已知∠1=30°,则∠2的大小是( )

|
| A. | 30° | B. | 45° | C. | 60° | D. | 65° |
一个几何体的三视图如图所示,则这个几何体是( )

|
| A. | 圆柱 | B. | 圆锥 | C. | 长方体 | D. | 正方体 |
 cm2
cm2


 边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.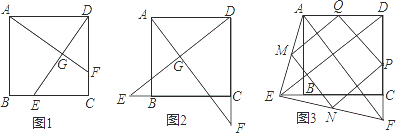

 x+b(b为常数且b<2)的垂线,垂足为点Q,则tan∠OPQ=
x+b(b为常数且b<2)的垂线,垂足为点Q,则tan∠OPQ=