题目内容
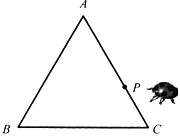
如图,是一个等边三角形木框,甲虫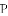
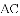
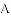
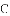
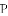
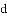
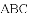
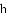
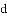
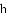
A. 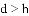
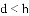
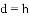
练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
题目内容
如图,是一个等边三角形木框,甲虫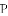
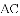
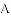
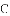
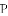
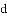
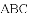
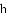
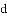
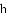

A. 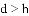
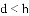
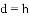
 智慧小复习系列答案
智慧小复习系列答案