题目内容
如图，在OABC中OA=a，AB=b，∠AOC=120°，则点C、B的坐标分别为________，________．
（-
b，
b） （a-b，b）
分析：根据已知条件求得∠COE=30°，CE=b，OE=b，OD=a-b，从而求得点C、B的坐标．
解答：
解：过点B作BD⊥x轴，设BC交y轴于点E，
∵∠AOC=120°，
∴∠COE=30°，
∵AB=b，
∴CE=b，OE=
=b，
∴点C的坐标为（-b，b），
∵OA=a，∴OD=a-b，∴点B的坐标为（a-b，b）．
点评：本题考查的知识点：点的坐标的求法、勾股定理．
b，b） （a-b，b）分析：根据已知条件求得∠COE=30°，CE=
b，OE=b，OD=a-b，从而求得点C、B的坐标．解答：
解：过点B作BD⊥x轴，设BC交y轴于点E，∵∠AOC=120°，
∴∠COE=30°，
∵AB=b，
∴CE=
b，OE==b，∴点C的坐标为（-
b，b），∵OA=a，∴OD=a-
b，∴点B的坐标为（a-b，b）．点评：本题考查的知识点：点的坐标的求法、勾股定理．
练习册系列答案
相关题目
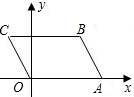如图，在OABC中OA=a，AB=b，∠AOC=120°，则点C、B的坐标分别为
（2012•漳州）如图，在?OABC中，点A在x轴上，∠AOC=60°，0C=4cm．OA=8cm．动点P从点O出发，以1cm/s的速度沿线段OA→AB运动；动点Q同时从点O出发，以acm/s的速度沿线段OC→CB运动，其中一点先到达终点B时，另一点也随之停止运动．设运动时间为t秒．
如图，在?OABC中，O（0，0），A（2，2），C（4，0），写出一个能将该平行四边形分成面积相等的两部分的直线的解析式：
OABC中，点A在x轴上，∠AOC=60o，OC=4cm．OA=8cm．动点P从点O出发，以1cm／s的速度沿线段OA→AB运动；动点Q同时从点O出发，以acm／s的速度沿线段OC→CB运动，其中一点先到达终点B时，另一点也随之停止运动．设运动时间为t秒．
OABC中，点A在x轴上，∠AOC=60o，OC=4cm．OA=8cm．动点P从点O出发，以1cm／s的速度沿线段OA→AB运动；动点Q同时从点O出发，以acm／s的速度沿线段OC→CB运动，其中一点先到达终点B时，另一点也随之停止运动．设运动时间为t秒．