题目内容
若两个正整数a、b的最大公约数比最小公倍数小23,且a≤b,则这样的数对(a,b)共有分析:根据题意先设a=mc,b=nc(m,n,c是正整数,且m,n互质),从而得到mnc-c=23,即c=
.再分两种情况讨论,当mn=24时和当mn=2时,就会得到这样的数对(a,b)共有3个.
| 23 |
| mn-1 |
解答:解:设a=mc,b=nc(m,n,c是正整数,且m,n互质),
则mnc-c=23,即c=
.
当mn=24时,则有这样的数对(3,8)(24,1);
当mn=2时,则有这样的数对(2,1);
经讨论可得有这样的数对3个.
故答案为:3.
则mnc-c=23,即c=
| 23 |
| mn-1 |
当mn=24时,则有这样的数对(3,8)(24,1);
当mn=2时,则有这样的数对(2,1);
经讨论可得有这样的数对3个.
故答案为:3.
点评:本题考查了最大公约数和最小公倍数,解题的关键是分类讨论,以防漏解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
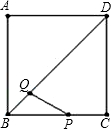 起点运动时,以PQ为直径的⊙O与直线BD的位置关系也随之变化,设运动时间为t(s).
起点运动时,以PQ为直径的⊙O与直线BD的位置关系也随之变化,设运动时间为t(s). cm/s.当其中一点到达自己的终点时,另一点也停止运动.当点P、点Q同时从各自的起点运动时,以PQ为直径的⊙O与直线BD的位置关系也随之变化,设运动时间为t(s).
cm/s.当其中一点到达自己的终点时,另一点也停止运动.当点P、点Q同时从各自的起点运动时,以PQ为直径的⊙O与直线BD的位置关系也随之变化,设运动时间为t(s).