Question

【题目】如图，矩形OABC的边OA，OC分别与坐标轴重合，并且点B的坐标为．将该矩形沿OB折叠，使得点A落在点E处，OE与BC的交点为D．

（1）求证：为等腰三角形；

（2）求点E的坐标；

（3）坐标平面内是否存在一点F，使得以点B，E，F，O为顶点的四边形是平行四边形，若存在，请直接写出点F的坐标；若不存在，请说明理由．

Answer 1

【答案】(1)见解析；(2) E点坐标为；(3)存在三点，，，

【解析】

（1）分析题目，证明OD=BD即可证明为等腰三角形，根据折叠的性质即可得到；

（2）根据矩形的性质先把OD的长度计算出来，再证明DE=CD，根据面积公式即可得到答案；

（3）分情况讨论点F所在的象限，根据平行四边形的性质计算即可得到．

解：（1）∵是由折叠所得，

∴≌，

∴，

又∵四边形OABC是矩形，

∴OA∥BC，

∴，

∴OD=BD

∴为等腰三角形

（2）过点E作EF⊥轴于F交BC于G，设CD的长为，则BD=BC-CD=8-，由（1）知OD=BD=8-，

∵四边形ABCD是矩形，,

∴∠OCD=∠OAB=90°，CA=AB，

∴在中，,

即，

解得，即CD=3，OD=BD=8-=5，

由(1)知，≌，

∴∠OEB=∠OAB=90°

∴∠OCD=∠BED=90°，

在和中，

,

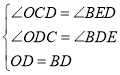∴≌（AAS），

∴DE=CD=3 ，BE=OC=4，

∵EF⊥轴，

∴∠OFB=90°，

∵OA∥BC，

∴∠CGE=∠OFB=90°,

∴CG⊥BD，

∴，

即，

∴在中，，

∵∠OCG=∠OFE=∠CGF =90°，

∴四边形OFGC是矩形，

∴OF=CG=CD+DG=3+=，

∴EF=GE+GF=+4=，

故E点坐标为；

(3) 存在三点，，

（附答案）可分三种情况：

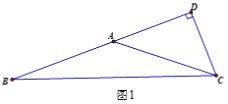
1．点F在第二象限，如图1：

∵，，，

∴，即；

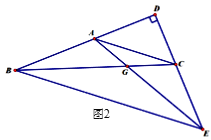
2．点F在第四象限，如图2：

∵，，，

∴，即；

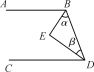
3．点F在第一象限，如图3：

∵，，，

∴，即；

故存在三点，，使得以点B，E，F，O为顶点的四边形是平行四边形．