题目内容
15.生活经验表明,靠墙摆放梯子时,若梯子底端离墙的距离约梯子长度的$\frac{1}{3}$,则梯子比较稳定.现有一长度为15米的梯子,当梯子稳定摆放时,梯子能到达的高度为多少米?它的顶端能否到达14米高的墙头?分析 在三角形ABC中利用勾股定理求解直角三角形即可.
解答 解:设梯子放平稳时,可以到达x米高的墙头,得
x2=152-(15×$\frac{1}{3}$)2.
解得:x=-10$\sqrt{2}$或x=10$\sqrt{2}$,
∵142=196<200,
∴它的顶端能到达14米高的墙头.
点评 考查了勾股定理的应用,解题的关键是熟练掌握勾股定理,基础知识比较简单.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
5.-(-2)的值是( )
| A. | -2 | B. | 2 | C. | ±2 | D. | 4 |
10.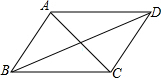 如图,已知四边形ABCD是平行四边形,下列结论中不一定正确的是( )
如图,已知四边形ABCD是平行四边形,下列结论中不一定正确的是( )
 如图,已知四边形ABCD是平行四边形,下列结论中不一定正确的是( )
如图,已知四边形ABCD是平行四边形,下列结论中不一定正确的是( )| A. | 当AB=AD时,它是菱形 | B. | 当AC=BD时,它是矩形 | ||
| C. | 当AC⊥BD时,它是菱形 | D. | 当∠ABC=90°时,它是正方形 |
7.函数y=4x的图象不经过的点的坐标是( )
| A. | (0,0) | B. | (1,4) | C. | (1,-4) | D. | (-1,-4) |
4.下列说法不正确的是( )
| A. | -ab2c的系数是-1,次数是4 | B. | $\frac{xy}{3}$-1是整式 | ||
| C. | 6x2-3x+1的项是6x2,-3x,1 | D. | 2πR+2π2是三次二项式 |
 如图,小华用一把含30°角的三角尺ABC绕直角顶点C顺时针旋转,使点A的对应点A′在边AB上.已知BC=6cm.
如图,小华用一把含30°角的三角尺ABC绕直角顶点C顺时针旋转,使点A的对应点A′在边AB上.已知BC=6cm.