题目内容
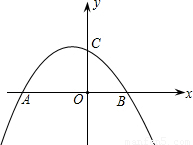
如图,抛物线y= 与x轴交于A、C两点,与y轴交于B点.
与x轴交于A、C两点,与y轴交于B点.

(1)求△AOB的外接圆的面积;
(2)若动点P从点A出发,以每秒1个单位沿射线AC方向运动;同时,点Q从点B出发,以每秒0.5个单位沿射线BA方向运动,当点P到底点C处时,两点同时停止运动.问当t为何值时,以A、P、Q为顶点的三角形与△OAB相似?
(3)若M为线段AB上一个动点,过点M作MN平行于y轴交抛物线于点N.问:是否存在这样的点M,使得四边形OMNB恰为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
解:(1)由题意得:A(6,0),B(0,-8),
∴OA=6,OB=8,
∴AB=10
∴S=π•(5)2=25π.
(2)设AP=t,则AQ=10-0.5t,
∵A(6,0),C(-2,0),
∴AC=8,
∴0≤t≤8
若△APQ∽△AOB,则 =
= .即∴t=
.即∴t= .
.
若△AQP∽△AOB,则 =
=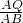 .∴t=
.∴t= >8(舍去)
>8(舍去)
∴当t= 时,以A、P、Q为顶点的三角形与△OAB相似.
时,以A、P、Q为顶点的三角形与△OAB相似.
(3)直线AB的函数关系式为y=x-8.
∵MN∥y轴,
∴设点M的横坐标为x,则M(x,x-8),N(x, x2-x-8).
x2-x-8).
若四边形OMNB为平行四边形,则MN=OB=8
∴(x-8)-( x2-x-8)=8,即x2-6x+12=0,
x2-x-8)=8,即x2-6x+12=0,
∵△<0,
∴此方程无实数根,
∴不存在这样的点M,使得四边形OMNB恰为平行四边形.
分析:(1)先求出AB两点的坐标,根据勾股定理得出AB的长,进而得出结论;
(2)设AP=t,则AQ=10-0.5t,再根据△APQ∽△AOB与△AQP∽△AOB两种情况进行讨论;
(3)设点M的横坐标为x,则M(x,x-8),N(x, x2-x-8),四边形OMNB为平行四边形,则MN=OB=8,再根据△<0即可得出结论.
x2-x-8),四边形OMNB为平行四边形,则MN=OB=8,再根据△<0即可得出结论.
点评:本题考查的是二次函数综合题,涉及到抛物线与x轴的交点问题、相似三角形的判定与性质等知识,难度适中.
∴OA=6,OB=8,
∴AB=10
∴S=π•(5)2=25π.
(2)设AP=t,则AQ=10-0.5t,
∵A(6,0),C(-2,0),
∴AC=8,
∴0≤t≤8
若△APQ∽△AOB,则
 =
= .即∴t=
.即∴t= .
. 若△AQP∽△AOB,则
 =
=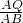 .∴t=
.∴t= >8(舍去)
>8(舍去)∴当t=
 时,以A、P、Q为顶点的三角形与△OAB相似.
时,以A、P、Q为顶点的三角形与△OAB相似.(3)直线AB的函数关系式为y=x-8.
∵MN∥y轴,
∴设点M的横坐标为x,则M(x,x-8),N(x,
 x2-x-8).
x2-x-8).若四边形OMNB为平行四边形,则MN=OB=8
∴(x-8)-(
 x2-x-8)=8,即x2-6x+12=0,
x2-x-8)=8,即x2-6x+12=0,∵△<0,
∴此方程无实数根,
∴不存在这样的点M,使得四边形OMNB恰为平行四边形.
分析:(1)先求出AB两点的坐标,根据勾股定理得出AB的长,进而得出结论;
(2)设AP=t,则AQ=10-0.5t,再根据△APQ∽△AOB与△AQP∽△AOB两种情况进行讨论;
(3)设点M的横坐标为x,则M(x,x-8),N(x,
 x2-x-8),四边形OMNB为平行四边形,则MN=OB=8,再根据△<0即可得出结论.
x2-x-8),四边形OMNB为平行四边形,则MN=OB=8,再根据△<0即可得出结论.点评:本题考查的是二次函数综合题,涉及到抛物线与x轴的交点问题、相似三角形的判定与性质等知识,难度适中.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 如图,抛物线y1与y2都与x轴交于点O(0,0)和点A,y1的顶点是B(2,-1),y2的顶点是C(2,-3),P是y1上的一个动点,过P作y轴的平行线交y2于点Q,分别过P,Q作x轴的平行线,分别交y1,y2于点P′,Q′,连接P′Q′.
如图,抛物线y1与y2都与x轴交于点O(0,0)和点A,y1的顶点是B(2,-1),y2的顶点是C(2,-3),P是y1上的一个动点,过P作y轴的平行线交y2于点Q,分别过P,Q作x轴的平行线,分别交y1,y2于点P′,Q′,连接P′Q′.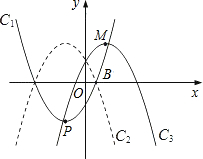 的左侧),点B的横坐标是1;
的左侧),点B的横坐标是1;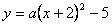 的顶点为P,与x轴相交于A、B两点(点A在点B的左侧),点B的横坐标是1。
的顶点为P,与x轴相交于A、B两点(点A在点B的左侧),点B的横坐标是1。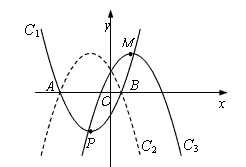
 与x轴交于A、B(A在B左侧),顶点为C(1,-2),
与x轴交于A、B(A在B左侧),顶点为C(1,-2),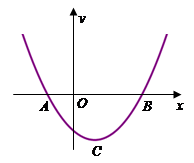
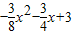 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.