题目内容
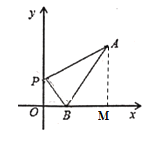
【题目】如图1,在平面直角坐标系中,![]() ,
,![]() ,且
,且![]() .
.
(1)求点A、B的坐标;
(2)如图1,P点为y轴正半轴上一点,连接BP,若![]() ,请求出P点的坐标;
,请求出P点的坐标;
(3)如图2,已知![]() ,若C点是x轴上一个动点,是否存在点C,使
,若C点是x轴上一个动点,是否存在点C,使![]() ,若存在,请直接写出所有符合条件的点C的坐标;若不存在,请说明理由.
,若存在,请直接写出所有符合条件的点C的坐标;若不存在,请说明理由.

【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() ,
,![]() ,理由见解析
,理由见解析
【解析】
(1)首先根据等式,可得出![]() 和
和![]() 的值,即可得出点A、B的坐标;
的值,即可得出点A、B的坐标;
(2)首先作![]() 轴于点M,设
轴于点M,设![]() ,且
,且![]() ,利用
,利用![]() ,列出等式,即可得出点P的坐标;
,列出等式,即可得出点P的坐标;
(3)根据题意,利用等腰三角形的性质,即可直接判定C的坐标,有两种情况,在x正半轴和负半轴上,即可得解.
解:(1)![]() ,
,![]()
∴![]() ,
,![]()
∴![]() ,
,![]()
(2)作![]() 轴于点M,如图所示
轴于点M,如图所示
设![]() ,且
,且![]()
∴![]()
![]()
若![]()
即![]()
∴![]()
∴![]()
(3)存在,![]() ,
,![]()
∵![]() ,
,![]() ,
,![]()
∴当C点在x正半轴上时,坐标为![]() ,
,
当C点在x负半轴上时,坐标为![]()
故答案为![]() ,
,![]() .
.

练习册系列答案
相关题目