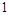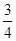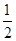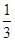题目内容
如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.
小题1:判断AE与⊙O的位置关系,并说明理由;
小题2:当BC=4,AC=3CE时,求⊙O的半径.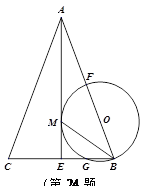
小题1:判断AE与⊙O的位置关系,并说明理由;
小题2:当BC=4,AC=3CE时,求⊙O的半径.

(1)
 与
与 相切
相切(2)
 的半径为
的半径为
解:(1) 与
与 相切.······················ 1分
相切.······················ 1分
理由如下:
连结 ,则
,则 .∴∠OMB=∠OBM.
.∴∠OMB=∠OBM.
∵ 平分
平分 ,∴∠OBM=∠EBM.
,∴∠OBM=∠EBM.
∴∠OMB=∠EBM.∴ .······················· 3分
.······················· 3分
∴ .
.
在 中,
中, ,
, 是角平分线,
是角平分线,
∴ .∴
.∴ .
.
\∴ .
.
∴ .∴
.∴  与
与 相切.····················· 4分
相切.····················· 4分
(2)在 中,
中, ,
, 是角平分线,
是角平分线,
∴ .
.
∵ ,∴
,∴ .
.
在 中,
中, ,∴
,∴ .
.
设 的半径为
的半径为 ,则
,则 .
.
∵ ,∴
,∴ .···················· 6分
.···················· 6分
 .
.  .
. .∴
.∴ 的半径为
的半径为 .
.
 与
与 相切.······················ 1分
相切.······················ 1分理由如下:
连结
 ,则
,则 .∴∠OMB=∠OBM.
.∴∠OMB=∠OBM.∵
 平分
平分 ,∴∠OBM=∠EBM.
,∴∠OBM=∠EBM.∴∠OMB=∠EBM.∴
 .······················· 3分
.······················· 3分∴
 .
.在
 中,
中, ,
, 是角平分线,
是角平分线,∴
 .∴
.∴ .
.\∴
 .
.∴
 .∴
.∴  与
与 相切.····················· 4分
相切.····················· 4分(2)在
 中,
中, ,
, 是角平分线,
是角平分线,∴
 .
.∵
 ,∴
,∴ .
.在
 中,
中, ,∴
,∴ .
.设
 的半径为
的半径为 ,则
,则 .
.∵
 ,∴
,∴ .···················· 6分
.···················· 6分 .
.  .
. .∴
.∴ 的半径为
的半径为 .
.
练习册系列答案
相关题目
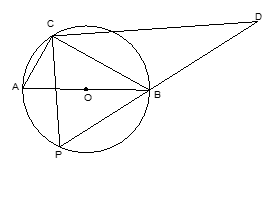
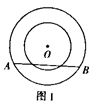
 中,
中, ,以AC为直径作
,以AC为直径作 ,交AB于D,过O作OE//AB,交BC于E,求证:ED为
,交AB于D,过O作OE//AB,交BC于E,求证:ED为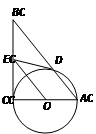
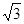 倍
倍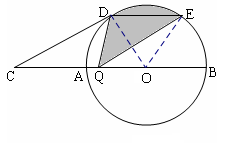
 上的点
上的点 (圆心
(圆心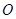 与点
与点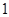 厘米/秒的速度向右运动(圆心
厘米/秒的速度向右运动(圆心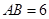 厘米,圆O、圆B的半径分别为
厘米,圆O、圆B的半径分别为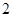 厘米.当两圆相交时,圆O的运动时间
厘米.当两圆相交时,圆O的运动时间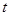 (秒)的取值范围是 .
(秒)的取值范围是 .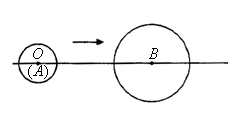
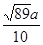 的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);
的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);

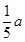 时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;
时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;