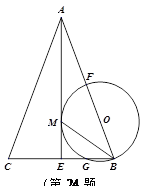
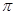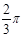题目内容
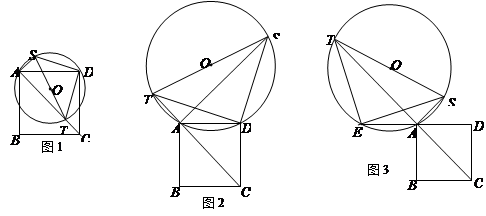
如图,在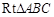 中,
中,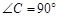 ,以AC为直径作
,以AC为直径作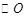 ,交AB于D,过O作OE//AB,交BC于E,求证:ED为
,交AB于D,过O作OE//AB,交BC于E,求证:ED为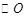 的切线.
的切线.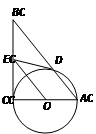
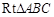 中,
中,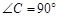 ,以AC为直径作
,以AC为直径作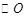 ,交AB于D,过O作OE//AB,交BC于E,求证:ED为
,交AB于D,过O作OE//AB,交BC于E,求证:ED为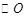 的切线.
的切线.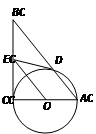
连OD,

∵OE//AB
∴∠EOC=∠A,∠EOD=∠ODA
又∵OA="OD"
∴∠A=∠ODA
∴∠EOC=∠EOD
又OE=OE OC=OD
∴△EOC≌△EOD
∴∠EDO=∠ECO 又∠C=90°
∴∠EDO=90°
即ED⊥DO 而点D在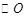 上 ∴ED为
上 ∴ED为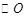 的切线
的切线

∵OE//AB
∴∠EOC=∠A,∠EOD=∠ODA
又∵OA="OD"
∴∠A=∠ODA
∴∠EOC=∠EOD
又OE=OE OC=OD
∴△EOC≌△EOD
∴∠EDO=∠ECO 又∠C=90°
∴∠EDO=90°
即ED⊥DO 而点D在
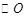 上 ∴ED为
上 ∴ED为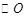 的切线
的切线连接OD,CD,求出∠BDC=90°,根据OE∥AB和OA=OC求出BE=CE,推出DE=CE,根据SSS证△ECO≌△EDO,推出∠EDO=∠ACB=90°即可

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
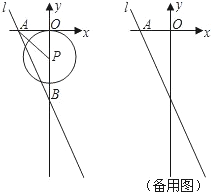
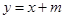 ,当直线PQ交y轴于Q,交⊙O于C、D两点时,过点C作CE垂直于x轴交⊙O于点E,过点E作EG垂直于y轴,垂足为G,过点C作CF垂直于y轴,垂足为F,连接DE.
,当直线PQ交y轴于Q,交⊙O于C、D两点时,过点C作CE垂直于x轴交⊙O于点E,过点E作EG垂直于y轴,垂足为G,过点C作CF垂直于y轴,垂足为F,连接DE.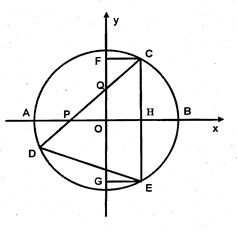
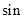 ∠CPB= ;
∠CPB= ;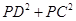 的值是否会发生变化?如果发生变化,请你说明理由;如果不发生变化,请你求出这个不变的值;
的值是否会发生变化?如果发生变化,请你说明理由;如果不发生变化,请你求出这个不变的值;