题目内容
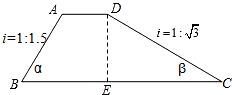 如图,拦水坝的横截面为梯形ABCD(图中i=1:
如图,拦水坝的横截面为梯形ABCD(图中i=1:| 3 |
(1)坡角α,β;
(2)求AB.
考点:解直角三角形的应用-坡度坡角问题
专题:
分析:(1)已知了斜坡AB的坡度,即可得到坡角α的正切值,由此可求得α的度数,同理求出坡角β的度数;
(2)已知了梯形的高,可过A作下底的垂线段,设垂足为F;在Rt△ABF中,根据铅直高度和坡度求得BF的长,再利用勾股定理即可求出AB.
(2)已知了梯形的高,可过A作下底的垂线段,设垂足为F;在Rt△ABF中,根据铅直高度和坡度求得BF的长,再利用勾股定理即可求出AB.
解答:解:(1)∵斜坡AB的坡度i=1:1.5,
∴tanα=
=
,
∴α≈33.69°;
∵斜坡CD的坡度i=1:
,
∴tanβ=
=
,
∴β=30°;
 (2)作AF⊥BC于F.
(2)作AF⊥BC于F.
∵
=i=
=
,AF=DE=6,
∴BF=
=9,
在Rt△ABF中,根据勾股定理得:
AB=
=3
.
∴tanα=
| 1 |
| 1.5 |
| 2 |
| 3 |
∴α≈33.69°;
∵斜坡CD的坡度i=1:
| 3 |
∴tanβ=
| 1 | ||
|
| ||
| 3 |
∴β=30°;
 (2)作AF⊥BC于F.
(2)作AF⊥BC于F.∵
| AF |
| BF |
| 1 |
| 1.5 |
| 2 |
| 3 |
∴BF=
| 3AF |
| 2 |
在Rt△ABF中,根据勾股定理得:
AB=
| AF2+BF2 |
| 13 |
点评:本题考查了解直角三角形的应用-坡度坡角问题,关键是设法化归为解直角三角形问题,必要时应添加辅助线,构造出直角三角形.

练习册系列答案
相关题目
 如图,该图形的面积是( )
如图,该图形的面积是( )A、
| ||
B、
| ||
| C、6xy | ||
| D、3xy |
根据下列表格的对应值
判断方程一元二次方程ax2+bx+c=0(a≠0,a、b、c为常数)一个解的范围是( )
| x | … | 3.3 | 3.4 | 3.5 | 3.6 | … |
| y=ax2+bx+c | … | -0.6 | -0.2 | 0.3 | 0.9 | … |
| A、3<x<3.3 |
| B、3.3<x<3.4 |
| C、3.4<x<3.5 |
| D、3.5<x<3.6 |
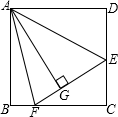 在正方形ABCD中,E、F分别是BC、CD上的点,∠EAF=45°,AG⊥EF,垂足为G,求证:AB=AG.
在正方形ABCD中,E、F分别是BC、CD上的点,∠EAF=45°,AG⊥EF,垂足为G,求证:AB=AG.
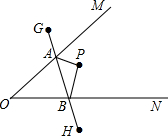 如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若GH的长为10cm,求△PAB的周长为
如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若GH的长为10cm,求△PAB的周长为