题目内容
19.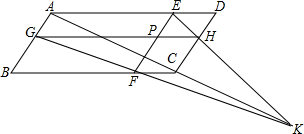 如图,设P为?ABCD内任意一点,过P作EF∥AB,GH∥BC,EF交A,BC于点E,F,GH交AB,DC于点G,H,且AC,GF,EH不平行.求证:AC,GF,EH相交于一点.
如图,设P为?ABCD内任意一点,过P作EF∥AB,GH∥BC,EF交A,BC于点E,F,GH交AB,DC于点G,H,且AC,GF,EH不平行.求证:AC,GF,EH相交于一点.
分析 先设AC、EH相交于点K,再证G、F、K三点共线,考虑到梅涅劳斯定理的逆定理,也就是证$\frac{CK}{KA}•\frac{AG}{GB}•\frac{BF}{FC}=1$,而由题设易知$\frac{AE}{ED}=\frac{BF}{FC}$,$\frac{DH}{HC}=\frac{AG}{GB}$,再结合△CAD与截线EHK使用梅涅劳斯定理可得$\frac{CK}{KA}•\frac{AE}{ED}•\frac{DH}{HC}=1$,结论是显然的.
解答 证明:设AC、EH相交于点K,
对于△CAD与截线EHK,由梅涅劳斯定理可得:$\frac{CK}{KA}•\frac{AE}{ED}•\frac{DH}{HC}=1$,
∵ABCD是平行四边形,且EF∥AB,GH∥BC,
∴$\frac{AE}{ED}=\frac{BF}{FC}$,$\frac{DH}{HC}=\frac{AG}{GB}$,
∴$\frac{CK}{KA}•\frac{AG}{GB}•\frac{BF}{FC}=1$,
由梅涅劳斯定理的逆定理可知G、F、K三点共线,
∴AC,GF,EH相交于一点.
点评 本题梅涅劳斯定理及其逆定理的经典应用,也是证明三线共点的一道代表性题目,难度不大,但值得研习.对于证明三线共点的题目,先让两线相交于一点,把问题转化为三点共线问题,也就是转化为线段比例问题,这样就容易入手.

练习册系列答案
相关题目
4.$\frac{1}{2015}$的相反数是( )
| A. | $\frac{1}{2015}$ | B. | -$\frac{1}{2015}$ | C. | 2015 | D. | -2015 |
11.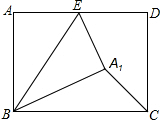 如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD的平分线上时,则AE的长为( )
如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD的平分线上时,则AE的长为( )
 如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD的平分线上时,则AE的长为( )
如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD的平分线上时,则AE的长为( )| A. | $\frac{5}{3}$或$\frac{5}{2}$ | B. | 2或3 | C. | $\frac{4}{3}$或$\frac{3}{2}$ | D. | 3或4 |
8.下列式子中,是分式的是( )
| A. | $\frac{8x}{3π}$ | B. | $\frac{{x}^{2}-{y}^{2}}{x-y}$ | C. | $\frac{x-y}{5}$ | D. | -$\frac{5}{8}$ |