题目内容
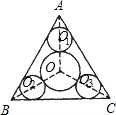 边长为1的正三角形ABC的中心O,以O为圆心,在正三角形内画一个圆,(⊙O),再作⊙O1,⊙O2,⊙O3,分别与正三角形的两边及⊙O都相切,试求,这四个面积总和的最大值与最小值,并指出面积总和取最值时对应的⊙O的半径.
边长为1的正三角形ABC的中心O,以O为圆心,在正三角形内画一个圆,(⊙O),再作⊙O1,⊙O2,⊙O3,分别与正三角形的两边及⊙O都相切,试求,这四个面积总和的最大值与最小值,并指出面积总和取最值时对应的⊙O的半径.
分析:设圆O的半径为x,已知圆O1,圆O2,圆O3的半径相等,设其为z,由AO1=2z,AO=
,得:3z+x=
,∴z=
-
,表示出四圆面积之和即可求出答案.
| ||
| 3 |
| ||
| 3 |
| ||
| 9 |
| x |
| 3 |
解答:解:设圆O的半径为x,已知圆O1,圆O2,圆O3的半径相等,设其为z,由AO1=2z,AO=
,
得:3z+x=
,
∴z=
-
,
设四个圆面积之和为y,则y=πx2+3π(
-
)2=
(x-
)2+
,
不难得到x的取值范围为
-3
≤x≤
,
∴x=
时,ymin=
,x=
时,ymax=
,
故当圆O的半径为
时,四圆面积和取最小值
;
当圆O的半径为
时,四圆面积和取最大值
.
| ||
| 3 |
得:3z+x=
| ||
| 3 |
∴z=
| ||
| 9 |
| x |
| 3 |
设四个圆面积之和为y,则y=πx2+3π(
| ||
| 9 |
| x |
| 3 |
| 4π |
| 3 |
| ||
| 12 |
| π |
| 12 |
不难得到x的取值范围为
| ||
| 3 |
| ||
| 4 |
| ||
| 6 |
∴x=
| ||
| 12 |
| π |
| 12 |
| ||
| 6 |
| π |
| 9 |
故当圆O的半径为
| ||
| 12 |
| π |
| 12 |
当圆O的半径为
| ||
| 6 |
| π |
| 9 |
点评:本题考查了相切两圆的性质,难度较大,关键是先求出x的取值范围,再确定y的最值.

练习册系列答案
相关题目
以边长为2厘米的正三角形的高为边长作第二个正三角形,以第二个正三角形的高为边长作第三个正三角形,以此类推,则第四个正三角形的边长是( )
A、3×(
| ||||
B、
| ||||
C、
| ||||
D、3×(
|
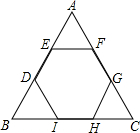 如图,木工师傅从一块边长为60cm的正三角形木板上锯出一块正六边形木板,那么这正六边形木板的边长为( )
如图,木工师傅从一块边长为60cm的正三角形木板上锯出一块正六边形木板,那么这正六边形木板的边长为( )| A、18cm | B、20cm | C、22cm | D、24cm |
 我们来探究“雪花曲线”的有关问题:如图(1)是边长为1的正三角形,将此三正角形的每条边三等分,而以居中的那一条线段为底边再作正三角形;然后以其两腰代替底边,得到第二个图形如图(2);再将图(2)的每条边三等分,并重复上述的作法,得到第三个图形如图(3),如此继续下去,得到的第五个图形的周长应等于
我们来探究“雪花曲线”的有关问题:如图(1)是边长为1的正三角形,将此三正角形的每条边三等分,而以居中的那一条线段为底边再作正三角形;然后以其两腰代替底边,得到第二个图形如图(2);再将图(2)的每条边三等分,并重复上述的作法,得到第三个图形如图(3),如此继续下去,得到的第五个图形的周长应等于 圆锥的轴截面是边长为6cm的正三角形ABC,P是母线AC的中点.求在圆锥的侧面上从B点到P点的最短路线的长.
圆锥的轴截面是边长为6cm的正三角形ABC,P是母线AC的中点.求在圆锥的侧面上从B点到P点的最短路线的长.