题目内容
3.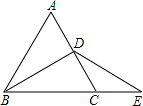 如图,△ABC是周长为6的等边三角形,BD长a为中线,E为BC延长线上的点,CE=CD,求△BDE的周长.
如图,△ABC是周长为6的等边三角形,BD长a为中线,E为BC延长线上的点,CE=CD,求△BDE的周长.
分析 根据等边三角形的性质可得CD=$\frac{1}{2}$AC,∠CBD=30°,再根据等腰三角形两底角相等和三角形的一个外角等于与它不相邻的两个内角的和列式求出∠E=30°,然后求出∠CBD=∠E,根据等角对等边可得BD=DE,然后根据三角形周长的定义列式计算即可得解.
解答 解:∵△ABC是周长为6的等边三角形,
∴BC=AC=6,
∵△ABC为等边三角形,BD是中线,
∴CD=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3,∠CBD=$\frac{1}{2}$×60°=30°,
∵CE=CD,
∴∠E=∠CDE=$\frac{1}{2}$×60°=30°,
∴∠CBD=∠E,
∴BD=DE=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∴△BDE的周长=6+3+3$\sqrt{3}$+3$\sqrt{3}$=9+6$\sqrt{3}$.
点评 本题考查了等边三角形的性质,等腰三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
13.下面关于基本事实和定理的联系的说法不正确的是( )
| A. | 基本事实和定理都是真命题 | |
| B. | 基本事实就是定理,定理就是基本事实 | |
| C. | 基本事实和定理都可以作为推理论证的依据 | |
| D. | 基本事实的正确性不需证明,定理的正确性需证明 |
13.下列说法中,正确的是( )
| A. | x=5是方程x+5=0的解 | B. | y=5是3y+15=0的解 | ||
| C. | z=-1是-$\frac{z}{4}$=4的解 | D. | x=0.04是方程25x=1的解 |
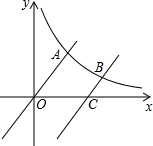 如图,已知函数y=x与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A,将y=x的图象向下平移6个单位后与双曲线y=$\frac{k}{x}$交于点B,与x轴交于点C.
如图,已知函数y=x与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A,将y=x的图象向下平移6个单位后与双曲线y=$\frac{k}{x}$交于点B,与x轴交于点C.