题目内容
如图所示，AB为⊙O的直径，P点为其半圆上一点，∠POA=40°，C为另一半圆上任意一点（不含A、B），则∠PCB＝ 度．
70°．
试题分析：根据平角定义，得∠BOP=180°-∠AOP=140°，再根据一条弧所对的圆周角等于它所对的圆心角的一半，得∠PCB=
∠POB=70°．试题解析：
∵∠POA=40°
∴∠BOP=180°-∠AOP=140°
∴∠PCB=
∠POB=70°．考点: 圆周角定理．
练习册系列答案
相关题目
试题分析：根据平角定义，得∠BOP=180°-∠AOP=140°，再根据一条弧所对的圆周角等于它所对的圆心角的一半，得∠PCB=
∠POB=70°．试题解析：
∵∠POA=40°
∴∠BOP=180°-∠AOP=140°
∴∠PCB=
∠POB=70°．考点: 圆周角定理．
为锐角
的外接圆，已知
，那么
的度数为 °．
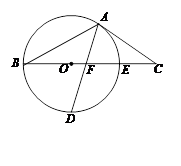
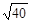，求⊙O的半径r．
，则弦AB所对的圆周角的度数为
