题目内容
【题目】已知![]() 是等边三角形,
是等边三角形,![]() 是
是![]() 上一点,
上一点,![]() 绕点
绕点![]() 逆时针旋转到
逆时针旋转到![]() 的位置.
的位置.
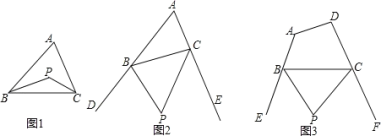
(1)如图,旋转中心是 ,![]() ;
;
(2)如图,如果![]() 是
是![]() 的中点,那么经过上述旋转后,点
的中点,那么经过上述旋转后,点 ![]() 转动了 度;
转动了 度;
(3)如果点![]() 为
为![]() 边上的三等分点,且
边上的三等分点,且![]() 的面积为
的面积为![]() ,那么四边形
,那么四边形![]() 的面积为 .
的面积为 .

【答案】(1)点A,60°;(2)60;(3)9或![]() .
.
【解析】
(1)根据等边三角形的性质得∠BAC=60°,再根据旋转的性质得旋转中心是点A,![]() ∠BAC=60°;
∠BAC=60°;
(2)利用对应关系确定![]() 的位置;
的位置;
(3)根据三角形面积公式求解.
解:(1)∵![]() 是等边三角形
是等边三角形
∴∠BAC=60°
∵![]() 绕点
绕点![]() 逆时针旋转到
逆时针旋转到![]() 的位置
的位置
∴旋转中心是点A,![]() ∠BAC=60°
∠BAC=60°
(2)∵AB和AC是对应边
∴经过上述旋转后,点![]() 转到了AC的中点位置,如图
转到了AC的中点位置,如图

∴![]() =60°
=60°
∴点![]() 转动了60°.
转动了60°.
(3)∵![]() 绕点
绕点![]() 逆时针旋转到
逆时针旋转到![]() 的位置
的位置
∴![]() ≌
≌![]()
∵BD=![]() BC或BD=
BC或BD=![]() BC
BC
∴CD=2BD或CD=![]() BD
BD
∴S△ABC=3S△ABD=3×3=9或S△ABC=![]() S△ABD=3×
S△ABD=3×![]() =
=![]()
∴S四边形ADCE= S△ABC=9或![]() .
.
故答案为(1)点A,60°;(2)60;(3)9或![]() .
.

练习册系列答案
相关题目
【题目】某商场用13000元购进甲、乙两种矿泉水共400箱,矿泉水的成本价与销售价如下表所示:
类别 | 成本价/(元·箱 | 销售价/(元·箱 |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这400箱矿泉水,可获利多少元?
【题目】经测算,某地气温![]() 与距离地面的高度
与距离地面的高度![]() 有如下对应关系:
有如下对应关系:
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| 26 | 20 | 14 | 8 |
| -4 | … |
请根据上表,完成下面的问题.
(1)猜想:距离地面的高度每上升![]() ,气温就下降______
,气温就下降______![]() ;表中
;表中![]() ______.
______.
(2)气温![]() 与高度
与高度![]() 之间的函数关系式是______.
之间的函数关系式是______.
(3)求该地距离地面![]() 处的气温.
处的气温.