题目内容
【题目】如图①,在矩形纸片ABCD中,AB= ![]() +1,AD=
+1,AD= ![]() .
.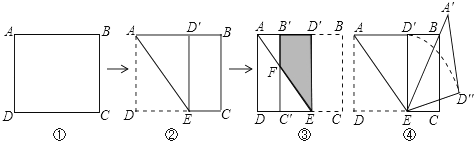
(1)如图②,将矩形纸片向上方翻折,使点D恰好落在AB边上的D′处,压平折痕交CD于点E,则折痕AE的长为 .
(2)如图③,再将四边形BCED′沿D′E向左翻折,压平后得四边形B′C′ED′,B′C′交AE于点F,则四边形B′FED′的面积为 .
(3)如图④,将图②中的△AED′绕点E顺时针旋转α角,得△A′ED″,使得EA′恰好经过顶点B,求弧D′D″的长 . (结果保留π)
【答案】
(1)![]()
(2)![]() ﹣
﹣ ![]()
(3)![]()
【解析】解:(1)∵△ADE反折后与△AD′E重合,
∴AD′=AD=D′E=DE= ![]() ,
,
∴AE= ![]() =
= ![]() =
= ![]() ;
;
⑵∵由(1)知AD′= ![]() ,
,
∴BD′=1,
∵将四边形BCED′沿D′E向左翻折,压平后得四边形B′C′ED′,
∴B′D′=BD′=1,
∵由(1)知AD′=AD=D′E=DE= ![]() ,
,
∴四边形ADED′是正方形,
∴B′F=AB′= ![]() ﹣1,
﹣1,
∴S梯形B′FED′= ![]() (B′F+D′E)B′D′=
(B′F+D′E)B′D′= ![]() (
( ![]() ﹣1+
﹣1+ ![]() )×1=
)×1= ![]() ﹣
﹣ ![]() ;
;
所以答案是:(1) ![]() ;(2)
;(2) ![]() ﹣
﹣ ![]() ;
;
⑶∵∠C=90°,BC= ![]() ,EC=1,
,EC=1,
∴tan∠BEC= ![]() =
= ![]() ,
,
∴∠BEC=60°,
由翻折可知:∠DEA=45°,
∴∠AEA′=75°=∠D′ED″,
∴ ![]() =
= ![]() .
.
【考点精析】利用勾股定理的概念和弧长计算公式对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.

【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别 | 成本价(元/箱) | 销售价(元/箱) |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?