题目内容
如图，在函数
(x＜0)和
(x＞0)的图象上，分别有A、B两点，若AB∥x轴且OA⊥OB，则A点坐标为 ．
（－
，
）
解析试题分析：由题意设A点坐标为（a，
），则可得B点坐标为（-4a，），由OA⊥OB即可根据勾股定理列方程求解.
由题意设A点坐标为（a，），则可得B点坐标为（-4a，）
∵OA⊥OB
∴
即
解得
因为点A在第二象限，
所以
，
所以A点坐标为（－，）.
考点：函数图象上的点的坐标的特征，勾股定理
点评：勾股定理是初中数学的重点，贯穿于整个初中数学的学习，是中考常见题，一般难度不大，需熟练掌握.
练习册系列答案
相关题目
如图，在函数y=| 1 |
| x |
| A、SA＜SB＜SC |
| B、SA＞SB＞SC |
| C、SA=SC=SB |
| D、SA＜SC＜SB |
式表示）
如图：在函数y=| 4 |
| x |
| A、矩形BCFG和矩形GAEP面积相等 |
| B、矩形FOEP和正方形COAB面积相等 |
| C、点B的坐标是（4，4） |
| D、图象关于过O、B两点的直线对称 |
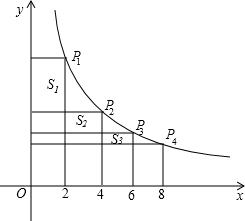
如图，在函数中 y=| 1 |
| x |
| A、S1＞S2＞S3 |
| B、S1＜S2＜S3 |
| C、S1＜S3＜S2 |
| D、S1=S2=S3 |
（2013•眉山）如图，在函数y1=