题目内容
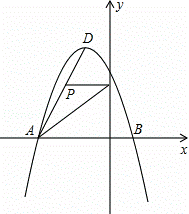
如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣3,0)、B(1,0)、C(0,3)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足点为E,连接AE.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果P点的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)在(2)的条件下,当S取到最大值时,过点P作x轴的垂线,垂足为F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P′,求出P′的坐标,并判断P′是否在该抛物线上.
解:(1)∵抛物线y=ax2+bx+c经过A(﹣3,0)、B(1,0)、C(0,3)三点,
∴ ,
,
解得  ,
,
∴解析式为y=﹣x2﹣2x+3
∵﹣x2﹣2x+3=﹣(x+1)2+4,
∴抛物线顶点坐标D为(﹣1,4).
(2)∵A(﹣3,0),D(﹣1,4),
∴设AD为解析式为y=kx+b,有  ,
,
解得 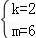 ,
,
∴AD解析式:y=2x+6,
∵P在AD上,
∴P(x,2x+6),
∴S△APE= •PE•yP=
•PE•yP=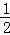 •(﹣x)•(2x+6)=﹣x2﹣3x(﹣3<x<﹣1),当x=﹣
•(﹣x)•(2x+6)=﹣x2﹣3x(﹣3<x<﹣1),当x=﹣ =﹣
=﹣ 时,S取最大值
时,S取最大值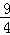 .
.
(3)如图1,设P′F与y轴交于点N,过P′作P′M⊥y轴于点M,
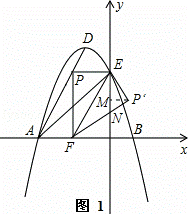
∵△PEF沿EF翻折得△P′EF,且P(﹣ ,3),
,3),
∴∠PFE=∠P′FE,PF=P′F=3,PE=P′E= ,
,
∵PF∥y轴,
∴∠PFE=∠FEN,
∵∠PFE=∠P′FE,
∴∠FEN=∠P′FE,
∴EN=FN,
设EN=m,则FN=m,P′N=3﹣m.
在Rt△P′EN中,
∵(3﹣m)2+( )2=m2,
)2=m2,
∴m= .
.
∵S△P′EN= •P′N•P′E=
•P′N•P′E= •EN•P′M,
•EN•P′M,
∴P′M=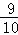 .
.
在Rt△EMP′中,
∵EM= =
=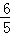 ,
,
∴OM=EO﹣EM=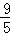 ,
,
∴P′ (
(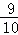 ,
,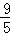 ).
).
当x=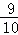 时,y=﹣(
时,y=﹣(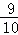 )2﹣2•
)2﹣2•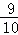 +3=
+3= ≠
≠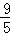 ,
,
∴点P′不在该抛物线上.

如图,在正方形ABCD中,对角线BD的长为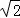 .若将BD绕点B旋转后,点D落在BC延长线上的点D′处,点D经过的路径为
.若将BD绕点B旋转后,点D落在BC延长线上的点D′处,点D经过的路径为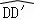 ,则图中阴影部分的面积是( )
,则图中阴影部分的面积是( )
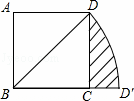
|
| A. |
| B. |
| C. |
| D. | π﹣2 |
 ﹣1
﹣1
 ﹣
﹣ 的自变量x的取值范围是
的自变量x的取值范围是  =
= .
. B.
B.  C.
C.  D.
D. 
 在实数范围内有意义,则x的取值范围是【 】
在实数范围内有意义,则x的取值范围是【 】 B.
B.  C.
C.  D.
D. 
 的解为
的解为