题目内容
如图,△![]() 是边长为6的等边三角形,
是边长为6的等边三角形, ![]() 是
是![]() 边上一动点,由
边上一动点,由![]() 向
向![]() 运动(与
运动(与![]() 、
、![]() 不重合),
不重合),![]() 是
是![]() 延长线上一动点,与点
延长线上一动点,与点![]() 同时以相同的速度由
同时以相同的速度由![]() 向
向![]() 延长线方向运动(
延长线方向运动(![]() 不与
不与![]() 重合),过
重合),过![]() 作
作![]() ⊥
⊥![]() 于
于![]() ,连接
,连接![]() 交
交![]() 于
于![]() .
.
(1)当∠![]() 时,求
时,求![]() 的长;
的长;
(2)在运动过程中线段![]() 的长是否发生变化?如果不变,求出线段
的长是否发生变化?如果不变,求出线段![]() 的长;如果发生改变,请说明理由.
的长;如果发生改变,请说明理由.
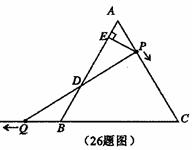
解: (1)(6分)解法一:过P作PE∥QC
 则△
则△![]() 是等边三角形,
是等边三角形,
∵P、Q同时出发、速度相同,即BQ=AP
∴BQ=PF
∴△![]() ≌△
≌△![]() ,
,
∴BD=DF
∵∠![]() ∠
∠![]() =∠
=∠![]() =∠
=∠![]() =
=![]() ,
,
∴BD=DF=FA=![]() AB=
AB=![]() =2,
=2,
∴AP=2.
解法二: ∵P、Q同时同速出发,∴AQ=BQ
设AP=BQ=![]() ,则PC=6-
,则PC=6-![]() ,QC=6+
,QC=6+![]()
在Rt△QCP中,∠CQP=![]() ,∠C=
,∠C=![]() ∴∠CQP=
∴∠CQP=![]()
∴QC=2PC,即6+![]() =2(6-
=2(6-![]() )
)
∴![]() =2
=2
∴AP=2
(2)由(1)知BD=DF
而△APF是等边三角形,PE⊥AF,
∵AE=EF
又DE+(BD+AE)=AB=6,
∴DE+(DF+EF)=6,
即DE+DE=6
∵DE=3为定值,即 DE的长不变

练习册系列答案
相关题目
 14、如图,O是边长为6的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于F,OE∥AC,交BC于E.则OD+OE+OF的值( )
14、如图,O是边长为6的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于F,OE∥AC,交BC于E.则OD+OE+OF的值( )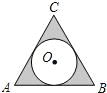 如图,⊙O是边长为2的等边三角形ABC的内切圆,则图中阴影部分的面积为
如图,⊙O是边长为2的等边三角形ABC的内切圆,则图中阴影部分的面积为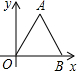 如图,△AOB是边长为5的等边三角形,则A,B两点的坐标分别是A
如图,△AOB是边长为5的等边三角形,则A,B两点的坐标分别是A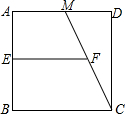 如图,M是边长为2cm的正方形ABCD的边AD的中点,E、F分别是AB、CM的中点.则EF=
如图,M是边长为2cm的正方形ABCD的边AD的中点,E、F分别是AB、CM的中点.则EF= 如图,△ABC是边长为6的等边三角形,AD=2,AE∥BC,直线BD交AE于点E,则BE的长为( )
如图,△ABC是边长为6的等边三角形,AD=2,AE∥BC,直线BD交AE于点E,则BE的长为( )