题目内容
已知：如图，BA=BD，BC=BE，∠ABD=∠CBE．
求证：AC=DE．
证明：∵∠ABD=∠CBE，
∴∠ABD+∠DBC=∠CBE+∠DCB，
即：∠ABC=∠DBE，
在△ABC和△DBE中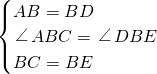
，
∴△ABC≌△DBE，
∴AC=DE．
分析：由SAS可判定△ABC≌△DBE，即可得出其对应线段相等．
点评：本题主要考查了全等三角形的判定及性质问题，能够熟练掌握．
∴∠ABD+∠DBC=∠CBE+∠DCB，
即：∠ABC=∠DBE，
在△ABC和△DBE中
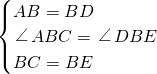，∴△ABC≌△DBE，
∴AC=DE．
分析：由SAS可判定△ABC≌△DBE，即可得出其对应线段相等．
点评：本题主要考查了全等三角形的判定及性质问题，能够熟练掌握．
练习册系列答案
相关题目
已知：如图，BA=BD，BC=BE，∠ABD=∠CBE．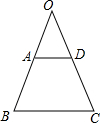
已知：如图，BA与CD相交于O，OA=OD，AD∥BC．求证：AB=CD．
