Question

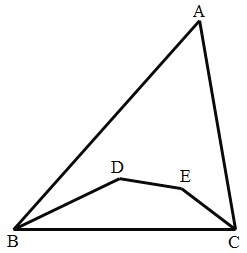
【题目】如图，△ABC 中，点 D,E 分别在∠ABC 和∠ACB 的平分线上，连接 BD,DE,EC,若∠D+∠E=295°， 则∠A 是（ ）

A.65°B.60°C.55°D.50°

Answer 1

【答案】D

【解析】

利用四边形BDEC的内角和为360°，即可求出∠DBC+∠ECB的度数，由BD、CE分别平分∠ABC、∠ACB可得∠ABC=2∠DBC, ∠ACB=2∠ECB，可求∠ABC+∠ACB

的度数，即可得∠A的度数.

解：在四边形BDEC中，∠DBC+∠EBC+∠D+∠E=360°

∵∠D+∠E=295°

∴∠DBC+∠ECB =360°-295°=65°

∵BD、CE分别平分∠ABC、∠ACB

∴∠ABC=2∠DBC, ∠ACB=2∠ECB

∴∠ABC+∠ACB=2∠DBC+2∠ECB=2(∠DBC+∠ECB)=130°

∴∠A=50°

故选：D