题目内容
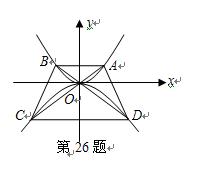
如图,点 在抛物线
在抛物线![]() 上,过点
上,过点![]() 作与
作与![]() 轴平行的直线交抛物线于点
轴平行的直线交抛物线于点![]() ,延长
,延长![]() 分别与抛物线
分别与抛物线![]() 相交于点
相交于点![]() ,连接
,连接![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,且
,且![]() 。
。
1.当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
2.当![]() 为何值时,四边形
为何值时,四边形![]() 的两条对角线互相垂直;
的两条对角线互相垂直;
3.猜想线段 与
与![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.

1.![]() 点
点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() ,
,![]()
![]() 点
点![]() 与点
与点![]() 关于
关于![]() 轴对称,
轴对称,![]() . 设直线
. 设直线 的解析式为
的解析式为![]() ,
,
![]()
解方程组 ,得
,得![]() .
.
2.当四边形![]() 的两对角线互相垂直时,由对称性得直线
的两对角线互相垂直时,由对称性得直线![]() 与
与![]() 轴的夹角等于
轴的夹角等于![]() 所以点
所以点![]() 的横、纵坐标相等,
的横、纵坐标相等,
这时,设![]() ,代入
,代入![]() ,得
,得![]() ,
,![]() .
.
即当![]() 时,四边形
时,四边形![]() 的两条对角线互相垂直.
的两条对角线互相垂直.
3.线段![]() 。
。
![]() 点
点![]() 在抛物线
在抛物线![]() ,且
,且![]() ,
,
得直线![]() 的解析式为
的解析式为![]() ,
,
解方程组 ,得点
,得点![]()
由对称性得点![]()
![]() ,
,
![]() .
.
解析:方程和不等式→二元一次方程组及解法;函数→一次函数的图像及性质; 函数→二次函数的图像及性质; 图形与证明→平行四边形、矩形、菱形、正方形的性质和判定定理;

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 在抛物线
在抛物线 上,过点
上,过点 轴平行的直线交抛物线于点
轴平行的直线交抛物线于点 ,延长
,延长 分别与抛物线
分别与抛物线 相交于点
相交于点 ,连接
,连接 ,设点
,设点 ,且
,且 .
.
 时,求点
时,求点 的坐标;
的坐标; 的两条对角线互相垂直;
的两条对角线互相垂直; 与
与 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.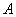 在抛物线
在抛物线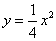 上,过点
上,过点 轴平行的直线交抛物线于点
轴平行的直线交抛物线于点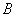 ,延长
,延长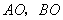 分别与抛物线
分别与抛物线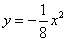 相交于点
相交于点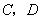 ,连接
,连接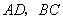 ,设点
,设点 ,且
,且 .
.
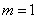 时,求点
时,求点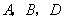 的坐标;
的坐标; 的两条对角线互相垂直;
的两条对角线互相垂直;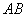 与
与 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
 上,过点
上,过点 轴平行的直线交抛物线于点
轴平行的直线交抛物线于点 ,延长
,延长 分别与抛物线
分别与抛物线 相交于点
相交于点 ,连接
,连接 ,设点
,设点 ,且
,且 .
. 时,求点
时,求点 的坐标;
的坐标; 的两条对角线互相垂直;
的两条对角线互相垂直; 与
与 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.