题目内容
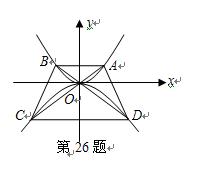
如图,点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 作与
作与![]() 轴平行的直线交抛物线于点
轴平行的直线交抛物线于点![]() ,延长
,延长![]() 分别与抛物线
分别与抛物线![]() 相交于点
相交于点![]() ,连接
,连接![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,且
,且![]() .
.
(1).当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2).当![]() 为何值时,四边形
为何值时,四边形![]() 的两条对角线互相垂直;
的两条对角线互相垂直;
(3).猜想线段![]() 与
与![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
解:(1)![]() 点
点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() ,
,![]() ,······························ 1分
,······························ 1分
![]() 点
点![]() 与点
与点![]() 关于
关于![]() 轴对称,
轴对称,![]() .························································ 2分
.························································ 2分
设直线![]() 的解析式为
的解析式为![]() ,
,
![]() .······················································································· 3分
.······················································································· 3分
解方程组 ,得
,得![]() .································································· 4分
.································································· 4分
(2)当四边形![]() 的两对角线互相垂直时,由对称性得直线
的两对角线互相垂直时,由对称性得直线![]() 与
与![]() 轴的夹角等于
轴的夹角等于![]() 所以点
所以点![]() 的横、纵坐标相等, 5分
的横、纵坐标相等, 5分
这时,设![]() ,代入
,代入![]() ,得
,得![]() ,
,![]() .
.
即当![]() 时,四边形
时,四边形![]() 的两条对角线互相垂直.········································· 6分
的两条对角线互相垂直.········································· 6分
(3)线段![]() .········································································································ 7分
.········································································································ 7分
![]() 点
点![]() 在抛物线
在抛物线![]() ,且
,且![]() ,
,
得直线![]() 的解析式为
的解析式为![]() ,
,
解方程组 ,得点
,得点![]() ······················································· 8分
······················································· 8分
由对称性得点![]() ,··················································· 9分
,··················································· 9分
![]() ,
,
![]() . 10分
. 10分
解析:略

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案 在抛物线
在抛物线 与
与
 在抛物线
在抛物线 上,过点
上,过点 轴平行的直线交抛物线于点
轴平行的直线交抛物线于点 ,延长
,延长 分别与抛物线
分别与抛物线 相交于点
相交于点 ,连接
,连接 ,设点
,设点 ,且
,且 .
.
 时,求点
时,求点 的坐标;
的坐标; 的两条对角线互相垂直;
的两条对角线互相垂直; 与
与 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.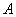 在抛物线
在抛物线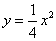 上,过点
上,过点 轴平行的直线交抛物线于点
轴平行的直线交抛物线于点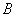 ,延长
,延长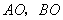 分别与抛物线
分别与抛物线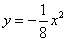 相交于点
相交于点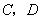 ,连接
,连接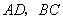 ,设点
,设点 ,且
,且 .
.
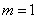 时,求点
时,求点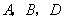 的坐标;
的坐标; 的两条对角线互相垂直;
的两条对角线互相垂直;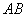 与
与 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
 上,过点
上,过点 轴平行的直线交抛物线于点
轴平行的直线交抛物线于点 ,延长
,延长 分别与抛物线
分别与抛物线 相交于点
相交于点 ,连接
,连接 ,设点
,设点 ,且
,且 .
. 时,求点
时,求点 的坐标;
的坐标; 的两条对角线互相垂直;
的两条对角线互相垂直; 与
与 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.